THE DIAGONAL SHAFTS IN THE GREAT PYRAMID
Upper southern shaft: 45°
Upper northern shaft: 32° 36'
Lower southern shaft: 39° 36'
Lower northern shaft: 39° 7'
Gantenbrink measured the angles of ascent of the upper (king's chamber) shafts all the way through, from inside and outside, and based on his survey data, he concluded that the intended slope of the upper southern shaft was 1/1 (45°) and that the intended slope of the upper northern shaft was 7/11 (32° 28' 16''). This slope for the upper northern shaft was within his narrowly defined margin of error for his survey data and it is exactly one half of the rise of the slope of the exterior faces of the pyramid (the height of 280 cubits over a half base of 220 cubits equals 14/11).
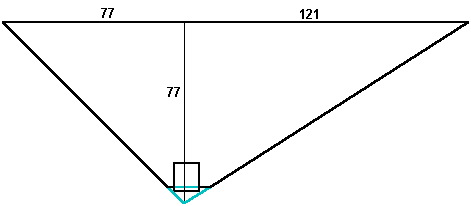
The King's chamber is 10 cubits wide. The north wall of the King's chamber is 16 cubits south of the vertical axis of the pyramid and the south wall of the chamber is 26 cubits south of the vertical axis of the pyramid. The shaft outlets are two cubits above the floor of the chamber, or 84 cubits above ground level. The northern shaft runs horizontally for five cubits before beginning it's ascent. The southern shaft runs horizontally for three cubits before beginning it's ascent. Extended downward, the intersection point of the shafts is five cubits below the floor of the chamber, or 77 cubits above ground level. This height is also 77 cubits below the height the shafts exit the pyramid. The intersection point is 22 cubits south of the vertical axis of the pyramid. 22 cubits south of the vertical axis of the pyramid is 77 cubits north of the point the southern shaft exits the pyramid and 121 cubits south of the point the northern shaft exits the pyramid. This gives sides of 77/121 (7/11) for the northern shaft as extended and 77/77 (1/1) for the southern shaft as extended.

Graham Chase observed that the vertical rise of the extended part of the shafts is 7 cubits and the horizontal run of the northern shaft is 11 cubits, while the horizontal run of the southern shaft is 7 cubits, demonstrating the rise and run of both shafts in the lowest possible whole numbers of cubits.
Robin Cook and John Legon observed that by extending the upper northern shaft beyond the face of the pyramid, it reaches the height of the apex of the pyramid 198 cubits north of it's exit point. This is a simple application of the 7/11 slope of the shaft: 126/198 = 7/11. Extended downward, the upper northern shaft intersects ground level 77 cubits north of the southern edge of the pyramid. The upper northern shaft intersects the southern face of the pyramid (as extended downward), 77 cubits south of the southern edge of the pyramid, 98 cubits below ground level. These points define a rectangle with a height equal to the height of the pyramid plus 98 cubits (below) and a width equal to the baselength of the pyramid plus 77 cubits on either side:

The diagonal of this rectangle is the upper northern shaft (as extended in both directions). The height of the rectangle is 378 cubits and the width is 594 cubits. The diagonal of the rectangle is 704 cubits: 378² + 594² = 704². Gantenbrink noted that many of the measures of the Great pyramid are multiples of 11. This width (54 x 11 = 594) and diagonal (64 x 11 = 704) are also multiples of 11.
Extended upward, the upper southern shaft intersects the height of the apex of the pyramid 126 cubits south of it's exit point: 126/126 = 1/1. This point is 72 cubits north of the southern edge of the rectangle. Extended downward, the upper southern shaft intersects ground level 55 cubits north of the midline of the pyramid. The upper southern shaft intersects the lower border of the rectangle 144 cubits south of it's northern edge. This point is also 54 cubits north of the exit point of the upper northern shaft. As extended downward, the upper shafts intersect below the king's chamber, 22 cubits south of the midline of the pyramid, 77 cubits above ground level and 77 cubits below the exit points of the upper shafts.
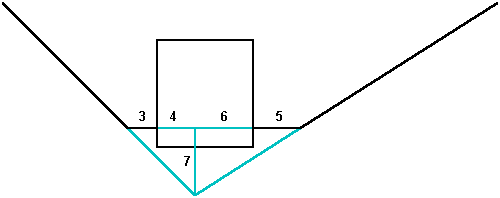
Unlike the upper shafts, the lower (queen's chamber) shafts do not exit the pyramid. Gantenbrink based his calculations of the angles of the lower shafts on measurements of less than one-half of the lower portion of the lower southern shaft and less than one-third of the lower portion of the lower northern shaft. Although there was a slight variance in Gantenbrink's survey data for the angles of the two lower shafts, Gantenbrink believes that the same slope may have been intended for these two shafts, making them symmetrical, since the queen's chamber is centered inside the pyramid. The shaft outlets in the queen's chamber are 44 cubits above ground level. The queen's chamber is 10 cubits wide and the shafts are horizontal for 3.7 cubits before beginning their angles of ascent. A slope of 9/11 equates to an angle of 39° 17' 22", in between Gantenbrink's survey data for the two lower shafts. With a slope of 9/11, the lower northern shaft, as extended upward beyond the pyramid, intersects the upper northern shaft at the height of the apex of the pyramid, 198 cubits north of the point the upper northern shaft exits the pyramid.

The 198 cubit square, centered just above the queen's chamber in the diagram above, has the same dimensions as the side lengths of the pyramid at the height of the exit points of the upper shafts. The upper southern shaft extended downward forms a diagonal from the upper southern corner to the lower northern corner of the square. The length of this diagonal is 280 cubits, equal to the height of the pyramid (198 x 1.4142 = 280). The lower southern shaft extended downward intersects the upper southern shaft at the lower northern corner of the square. [4] The lower northern shaft extended downward intersects the lower southern corner of the square. As extended downward 98 cubits below ground level, the lower northern shaft intersects the lower border of the outside rectangle 55 cubits north of the southern edge of the pyramid. The distance of the lower northern shaft extended in both directions is 378 cubits up and 462 cubits across, a slope of 9/11.
Both of the lower shafts intersect the sides of the square 36 cubits below the upper shaft exit points and both of the lower shafts as extended upward cross over the height of the upper shaft exit points 44 cubits across from the exit points, also showing a slope of 9/11 (36/44). The upper northern shaft as extended downward also crosses ground level 44 cubits south of the exit point of the upper southern shaft. 56 cubits below the height of the upper shaft exit points, the faces of the pyramid are also 44 cubits across from the points where the upper shafts exit the pyramid, expressing the slope of the exterior faces: 14/11 = 56/44 = 280/220.
The point on the midline of the pyramid at groundlevel is the origin point of the arc in the diagram. The height of the upper shaft exit points is 154 cubits above ground level. The points where the lower shafts cross directly under the upper shaft exit points, are also 154 cubits from the midline of the pyramid at ground level. The distance of these diagonals may be calculated as the hypoteneuse of the right triangle formed by the height above ground level where the lower shafts cross under the upper shaft exit points (118 cubits) and the distance across from this point to the centerline of the pyramid (99 cubits): 118² + 99² = 154².
The two lower shafts intersect at the midline of the pyramid, 37 cubits above ground level and 81 cubits above the lower border of the square. This point is also 81 cubits below the point where the lower shafts intersect the sides of the square. The sides of the square are 99 cubits across from the intersection point of the lower shafts, demonstrating the same ratio as the slope of the lower shafts (81/99 = 9/11). All of the measures in the diagram above are integers and they are all multiples of 7, 9 and/or 11, supporting the proposed design specifications of 7/11, 9/11 and 11/11 for the diagonal shafts.
Michael Saunders recently proposed that in addition to the slope of the Great Pyramid, there is also a trigonometric relationship between the slopes of the shafts and π. The vertical axis of the pyramid is 280 cubits and the horizontal axis is 220 cubits (half-base). This proportion reduces to 14/11. Given a value of 22/7 for π , 14/11 is equal to 4/π. Since the tangent identity is the proportion between the vertical and the horizontal axis of a right triangle, the inverse tangent of 4/π is equal to the angle of the pyramid.

The 7/11 slope of the upper northern shaft is equal to 2/π . The inverse tangent of 2/π is equal to the angle of this shaft.
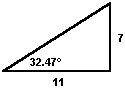
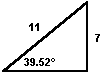
The sine identity is the proportion between the vertical axis and the hypotenuse of a right triangle. The observed angles of the lower shafts approximate the inverse sine of 2/π, making the proportion between the vertical axis and the hypotenuse of the lower shafts the same as the proportion between the vertical and the horizontal axis of the upper northern shaft. A vertical axis of 7 and a hypotenuse of 11 gives a horizontal axis equal to the square root of 72.
See Also:
Shaft Geometry and Astronomical Alignments