GEOMETRY IN THE GREAT PYRAMID

The external dimensions of the pyramid, the dimensions of the
inclined passages and the shafts, and the heights of the chambers and the horizontal
passages in the vertical crossection of the pyramid are all derived from two
geometric constructions. The first is a division of the half base of the pyramid
into the golden section. The second is a division of the height of the pyramid
by the square root of two
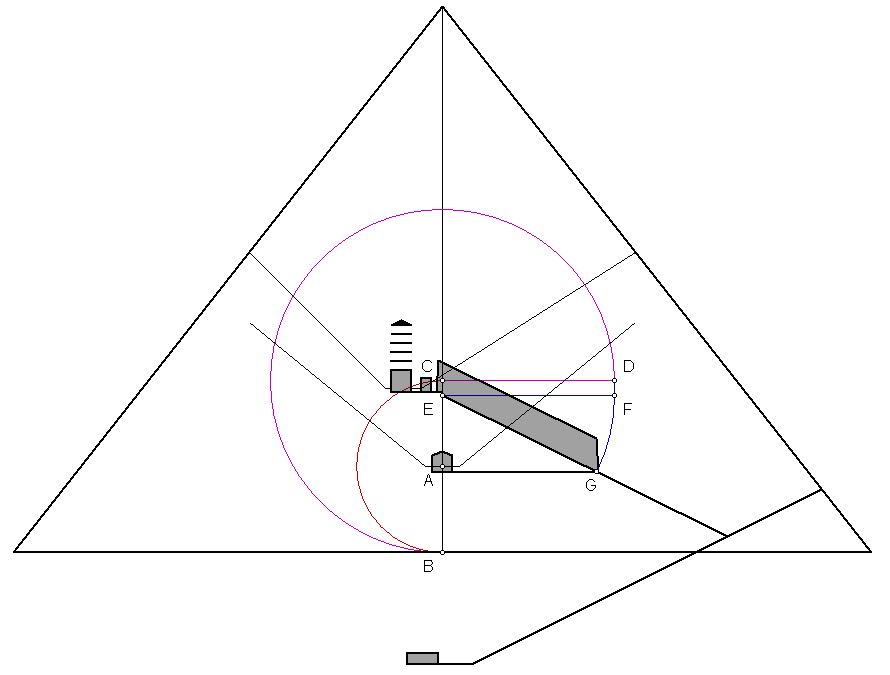
Draw line BC and construct the midpoint at D. Construct a perpendicular line from
point D. Arc DB to point E. Construct the midpoint of CD at point F. Arc FE to
point G. Arc CG to point A. Given a length of 440 cubits for BC, the length of
AD is 280 cubits and the lengths of AB and AC are 356 cubits. Point G divides
the half base (BD) into golden section segments of 84 cubits (BG) and 136 cubits
(DG). Construct a perpendicular line from point G, arc GB to the line and construct
horizontal line to point I. This is the height of the horizontal sections of the
shafts in the king's chamber. Arc DG to point H, 136 cubits above the base of
the pyramid. Extended to the southern face of the pyramid, the floor of the ascending
passage and the grand gallery cuts the southern face of the pyramid 136 cubits
above the base of the pyramid. The length of AH is 144 cubits.
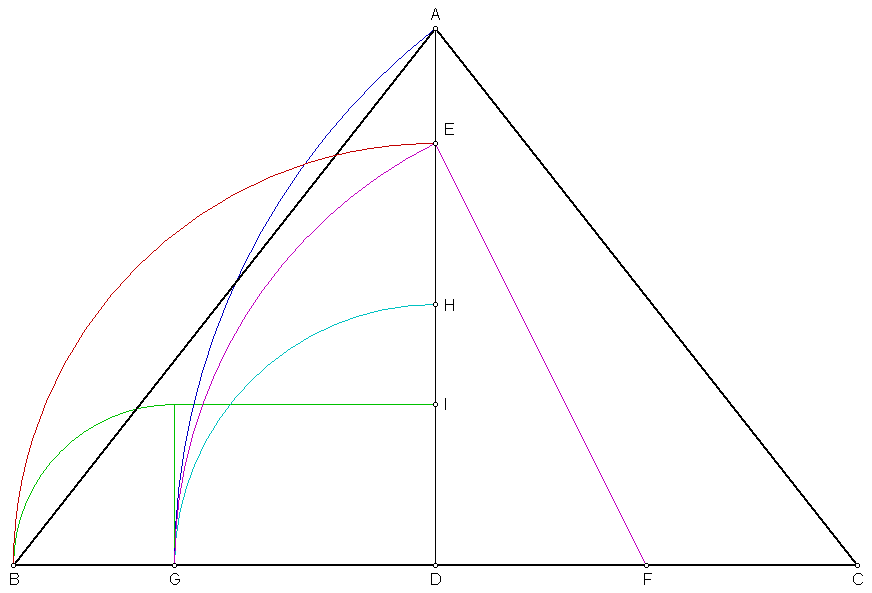
Construct the midpoint of AB at C. Construct a perpendicular line from point C
and arc CA to point D. Arc AD to point E. Given a length of 280 cubits for AB,
AD and AE are198 cubits and BE is 82 cubits. 198 cubits is equal to the height
of 280 cubits divided by the square root of two. The height of the floor of the
king's chamber, the antechamber, and the horizontal passages connecting the grand
gallery to the antechamber and the king's chamber is 82 cubits.

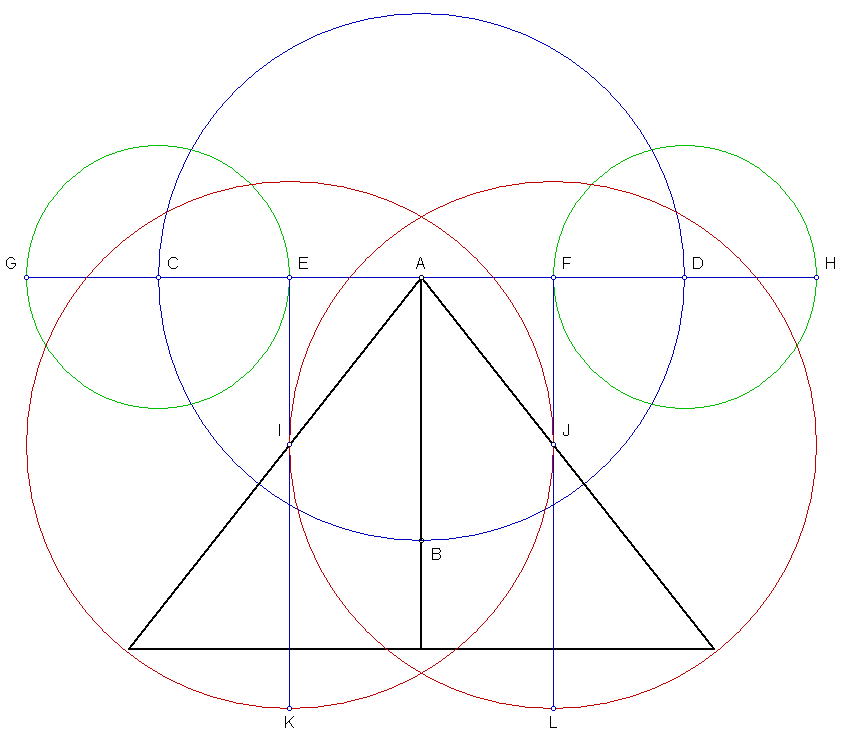
Construct a horizontal line through point A. Construct a circle with radius AB
(198 cubits), intersecting the horizontal line at points C and D. Construct the
midpoint of AC at point E. Construct the midpoint of AD at point F. Construct
circle with radius CE, intersecting the horizontal line at point G. Construct
circle with radius DF, intersecting the horizontal line at point H. Construct
vertical lines at points E and F, intersecting the sloping faces of the pyramid
triangle at points I and J. Construct circle with radius I J, intersecting the
vertical line from point E at point K. Construct circle with radius J I, intersecting
the vertical line from point F at point L. The horizontal distance between points
I and J is 198 cubits. The height of I and J above the base of the pyramid is
154 cubits. Points I and J are the points that the king's chamber shafts exit
the north and south faces of the pyramid. Points K and L are 198 cubits below
points I and J, or 44 cubits below the base of the pyramid triangle.
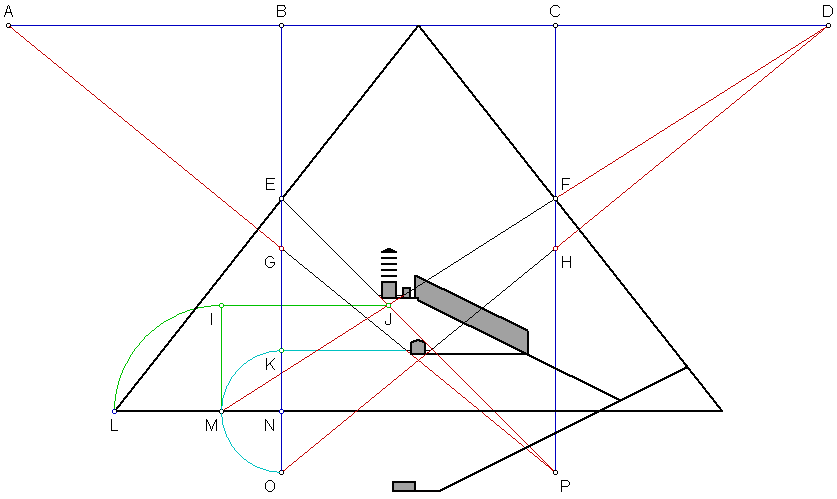
AB, BC and CD are each 198 cubits long. Points E and F are located at the points
where the king's chamber shafts exit the pyramid. EF and FP are each 198 cubits
in length, producing an angle of 45°
for EP, matching the angle of the southern king's chamber shaft. CF
is 126 cubits and CD is 198 cubits. 126/198 is a slope of 7/11 or an angle of
32° 28' 16", matching
the angle of the northern king's chamber shaft. DF extended downward intersects
ground level at point M, 77 cubits from the southern edge of the pyramid triangle.
Construct a vertical line from M and arc ML to point I. This is the height of
the intersection point of the king's chamber shafts, extended downward (point
J). BO and CP are 324 cubits long. AC and BD are 396 cubits long. 324/396 is a
slope of 9/11 or an angle of 39°
17' 22" for lines AP and D0. These lines correspond to the locations and
angles of the queens chamber shafts. The upper ends of the queen's chamber shafts
terminate at points G and H, 118 cubits above the base of the pyramid. This is
halfway between the 82 cubit height of the floor of the king's chamber and the
154 cubit height of the exit points of the king's chamber shafts. MN is 44 cubits.
This is the same distance that point O is below the base of the pyramid. Arc NO
through point M to point K. This is the height of the lower horizontal sections
of the queen's chamber shafts.
Point A is the previously constructed golden section segment on the half base
of the pyramid, 136 cubits above the base. The midway point on vertical lines
between the exit points of the king's chamber shafts and the upper ends of the
queen's chamber shafts is also 136 cubits above ground level. Construct a horizontal
line through point A, intersecting the southern face of the pyramid at point B.
Construct a horizontal line through the exit points of the king's chamber shafts,
154 cubits above the base of the pyramid. Construct a vertical line through point
B, intersecting the horizontal line from the king's chamber shaft exit points
at point C and intersecting the base of the pyramid at point D. The length of
CD is 154 cubits. Arc CD to point E and arc EC to point F. The length of CF is
308 cubits. Construct a vertical line from point F to the horizontal line through
point A at point G. The length of BG is 308 cubits. This is the length of the
ascending passage and the grand gallery as extended from the southern face of
the pyramid to ground level. Arc BG to point H where it intersects of the base
of the pyramid. BH crosses the midline of the pyramid 80.3 cubits above ground
level. This is the height of the end of the floor of the grand gallery at the
bottom of the great step at the midline of the pyramid. The angle of the ascending
passage and the grand gallery that is produced by this construction is 26.20°,
the surveyed angle of the ascending passage and the grand galllery.

The length of the floor of the grand gallery from the north wall to the great
step at the midline of the pyramid is 88 cubits. The height of the horizontal
sections of the queen's chamber shafts is 44 cubits. Point A is at the height
of the horizontal sections of queen's chamber shafts. Arc AB to point C, 88 cubits
above ground level on the midline of the pyramid. Construct a horizontal line
from C and arc CB to point D. The floor of the grand gallery ends at the bottom
of the great step at the midline of the pyramid at point E. Construct a horizontal
line from point E and construct a vertical line from point D intersecting the
horizontal line from point E at point F. Arc EF to point G on the previously constructed
line of the floor of the grand gallery and the ascending passage. The ascending
passage ends and the grand gallery begins at point G. The floor of the horizontal
queen's chamber passage is also at the height of point G.
Point B is the previously constructed golden section segment on the half base
of the pyramid, 136 cubits above the base. AB is 144 cubits. Construct a horizontal
line from point A and arc AB to point C. Construct a vertical line from point
C to the base of the pyramid at point D. Arc AD to the northern face of the pyramid.
Point E is 32.4 cubits above the base of the pyramid. This is the height of the
floor of the descending passage on the northern face of the pyramid. Construct
a horizontal line from point E and a vertical line from point E to the base of
the pyramid at point F. Construct circle EF and mark point G on the horizontal
axis. Construct circle GE and mark point H on the horizontal axis. Construct a
vertical line from point H to the base of the pyramid at point I. The slope of
EI is one over two or 26.565°,
the surveyed angle of the descending passage. Point J is the beginning point of
the horizontal passage that leads to the king's chamber, at the midline of the
pyramid 82 cubits above ground level. The straight line distance from point E
to point J is 200.7 cubits. This is within one tenth of one cubit of the surveyed
length of the descending passage. Arc EJ to the point where it intersects the
line of the descending passage at point K. This point marks the end of the descending
passage and the beginning of the horizontal passage that leads to the subterranean
chamber. Based on this construction, the distance from the beginning of the descending
passage to the point where the extended floor of the ascending passage intersects
the floor of the descending passage is 53.9 cubits, equal to the surveyed distance
for this part of the descending passage.

BACK