KING'S CHAMBER SHAFTS GEOMETRY
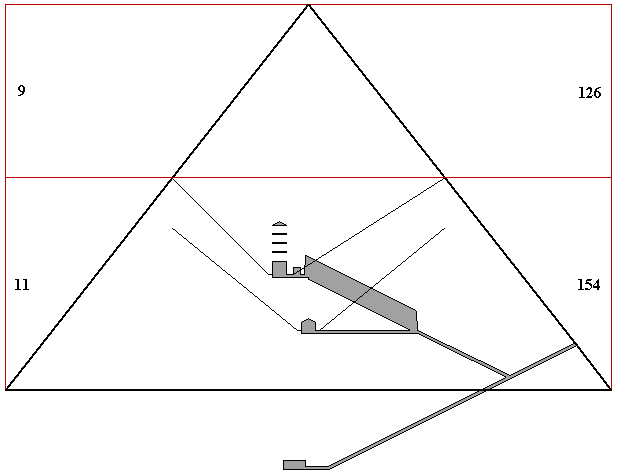
The south wall of the King's chamber is 26 cubits south of the midline of the pyramid. The ceiling of the southern shaft is 84 cubits above ground level at the south wall of the King's chamber. The southern shaft begins it's angle of ascent three cubits south of the southern wall of the King's chamber. In 1993, Rudolph Gantenbrink used a specially designed robot to measure the angle of incline along the entire length of the shaft and found the mean angle to be 45°, or a slope of 1/1. Given 280 cubits for the completed height and 440 cubits for the baselength of the pyramid, and the measurements of the shaft given above, the length of the ascending portion of the shaft to the outer casing of the pyramid is 99 cubits. The horizontal and vertical distance of the ascending portion of the shaft is 70 cubits, and the ceiling of the shaft exits the outer casing of the pyramid 154 cubits above ground level.
The north wall of the King's chamber is 16 cubits south of the midline of the pyramid. The ceiling of the northern shaft is 84 cubits above ground level at the north wall of the King's chamber. The northern shaft begins its angle of ascent five cubits north of the northern wall of the King's chamber. Gantenbrink measured the angle of ascent along the entire length of the shaft. The lower portion of the northern shaft is constructed around the grand gallery and Gantenbrink found variations in the angle of incline in this short portion of the shaft. Gantenbrink numbered the ceiling blocks in the shaft. The first block is the five cubit horizontal section. Ceiling blocks 2-6 are the part of the shaft that goes around the grand gallery. Gantenbrink found that the angle of ascent from block six to the point the shaft exits the pyramid is 32.6°. Gantenbrink found the mean angle of the entire inclined portion of the shaft to be a slope of 7/11 or an angle of 32.47°. Given the exterior dimensions of the pyramid and the measurements of the shaft given above, the vertical distance of the ascending portion of the shaft is 70 cubits, the horizontal distance is 110 cubits, and the ceiling of the shaft exits the outer casing of the pyramid 154 cubits above ground level.
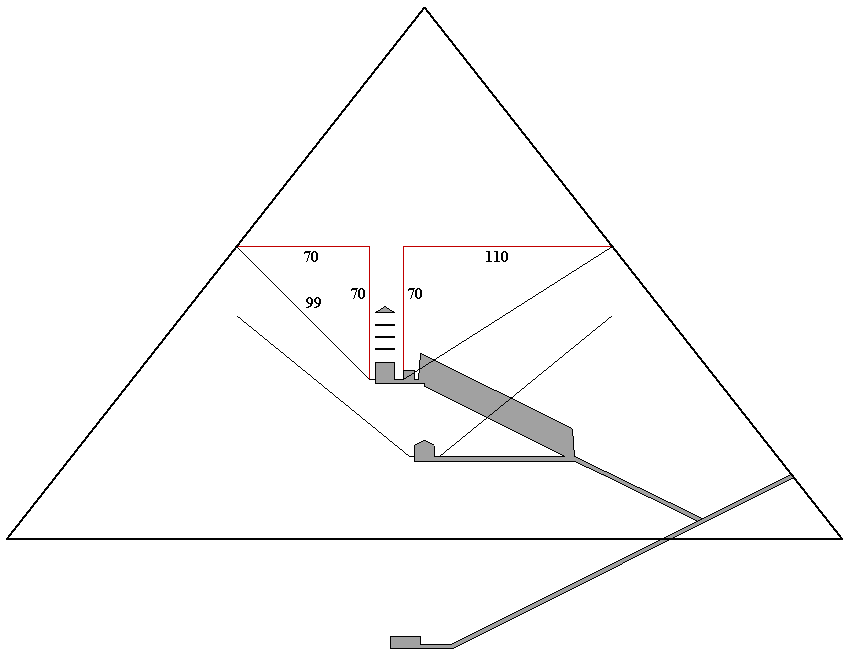
Extended downward, the two King's chamber shafts intersect seven cubits below the point they begin their ascent. The extended portions of the shafts show the slopes of both shafts in the lowest common denomination of whole numbers of cubits: 7/7 for the southern shaft and 7/11 for the northern shaft.
The rise and run of the inclined parts of the shafts are 10x multiples of the slopes of 7/7 (70/70) and 7/11 (70/110). The rise and run of the shafts from the intersection point to the point the shafts exit the pyramid are 11x multiples of the slopes (77/77 and 77/121). The slope of the pyramid is 14/11 (280/220). The 7/11 slope of the southern shaft is one-half of the slope of the pyramid. The intersection point is 77 cubits above ground level and 77 cubits below the height the shafts exit the pyramid. The intersection point is 22 cubits south of the midline of the pyramid and seven cubits below the height of the shafts in the king's chamber, producing a right triangle with sides in the ratio of 22/7. The sidelength of the pyramid 154 cubits above ground level is 198 cubits (77 + 121), equal to the vertical distance from the apex of the pyarmid to the floor of the King's chamber (280-82). 198 cubits is also equal to the height of the pyramid divided by the square root of 2 (280/1.4142 = 198). Thus, the horizontal area of the pyramid 154 cubits above ground level is equal to one-half of the square area of the height of the pyramid. Because the area of the faces of the pyramid are equal to the area of the square height of the pyramid, the horizontal area of the pyramid 154 cubits above ground level is also equal to one-half of the area of the faces of the pyramid.
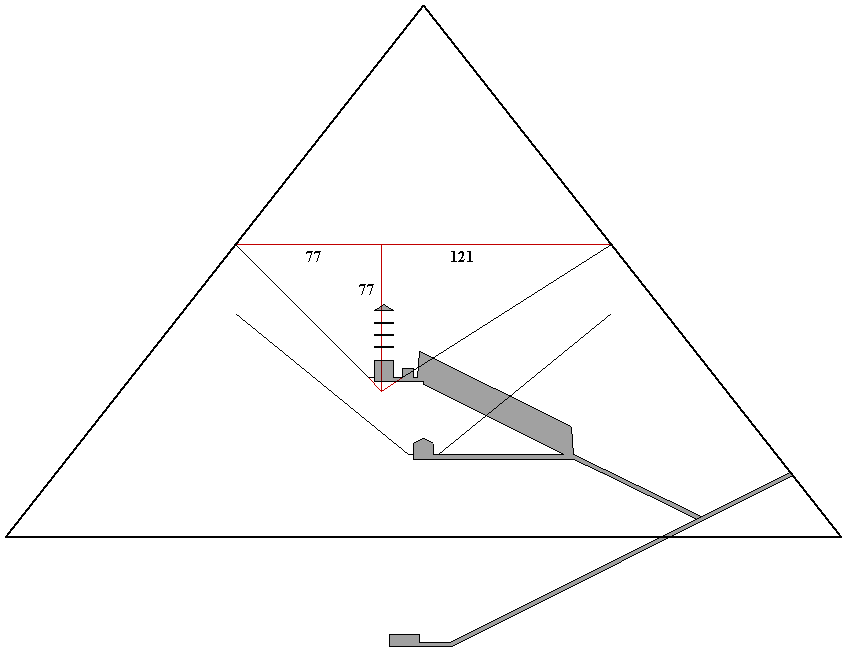
The height of the pyramid up from the exit points of the shafts is 126 cubits (280-154). Extended upward, the northern shaft intersects the height of the pyramid 198 cubits horizontally from the point the northern shaft exits the pyramid (198 x 7/11 = 126).The 99 cubit length of the ascending part of the southern shaft is one-half of the 198 cubit sidelength of the pyramid 154 cubits above ground level. The horizontal distance from the shafts intersection point to the point the southern shaft exits the pyramid is 121 cubits. The horizontal distance from the exit points to the outer edges of the pyramid at ground level are also 121 cubits (121 x 14/11 = 154). Extended downward, the northern shaft intersects ground level 77 cubits north of the southern edge of the pyramid and 121 cubits south of the intersection of the shafts. The northern shaft intersects the southern face of the pyramid 77 cubits south of the southern edge of the pyramid. Extended upward, the southern shaft intersects the height of the pyramid 72 cubits north of the intersection point of the northern shaft and the southern face of the pyramid. Extended downward, the southern shaft intersects the level of the intersection of the northern shaft and the southern face of the pyramid 144 cubits south of the intersection of the northern shaft and the height of the pyramid. The shafts exit the king's chamber and begin their angle of ascent 84 cubits above ground level, or 196 cubits below the apex. 84 cubits above ground level, the half base of the pyramid is 154 cubits. The intersection of the shafts, extended downward vertically, divides the 440 cubit baselength of the pyramid at ground level in the ratio of 198/242, or 9/11.

QUEEN'S CHAMBER SHAFTS GEOMETRY
The south wall of the queen's chamber is five cubits south of the midline of the pyramid and the north wall is five cubits north of the midline. The ceilings of the queen's chamber shafts are 44 cubits above ground level at the walls of the chamber. According to Gantenbrink, the southern shaft begins it's angle of ascent 1.96 meters south of the southern wall and the northern shaft begins it's antle of ascent 1.93 meters north of the north wall. Based on 24 measurements over a distance of 28 meters, Gantenbrink found the southern shaft to be inclined at a mean angle of 39.6°. After approximately 18 meters, the northern shaft bends to go around the grand gallery. Gantenbrink's robot was only able to measure this part of the northern shaft because the robot could not traverse the bend. Gantenbrink found a range of angles from 33.3° to 40.1° for the inclined part of the shaft below the bend. Gantenbrink gave an estimated mean angle for the northern shaft of 39.1°, but he gave a margin of error of two degrees for his estimate of the southern shaft and concluded that the angle of the shaft would need to be surveyed above the bend to determine if the angle of both shafts was intended to be the same. According to Gantenbrink, the first stone blocking the upper end of the southern shaft is 59.4 meters from the queen's chamber.
In 2003, Zahi Hawass conducted further robotic explorations of both of the queen's chamber shafts. Hawass found another blocking stone in the northern shaft. Hawass reported that the distance from the queens' chamber to the blocking stones was 208 feet for both shafts. Hawass also reported that the blocking stones were both in the same relative locations inside the pyramid.
A slope of 9/11 equally divides the difference between the slopes of the king's chamber shafts:
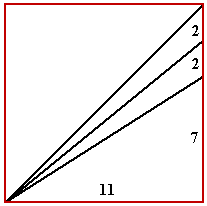
The overall east-west and north-south distance of the Giza site is in the ratio of 9/11:

The exit points of the king's chamber shafts divide the height of the pyramid in the ratio of 9/11:
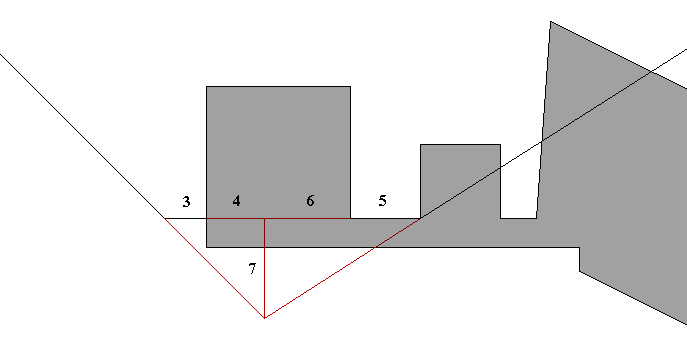
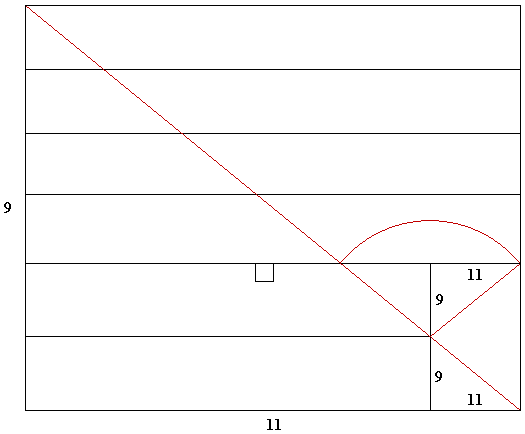
The queen's chamber shafts are in the north and south walls of the chamber. The north and south walls of the chamber are 9 cubits high and 11 cubits long. The doorway, the shaft and the course heights of the north wall of the queen's chamber are diagramed below according to WMF Petrie's measurements. The diagonal of the north wall shows the 9/11 ratio between the height of the first two courses and the width of the doorway.
In the diagram below, the slope of the queen's chamber shafts is 9/11 or an angle of 39.29°. John Legon and Robin Cook both suggested that the queen's chamber northern shaft, extended upward, intersects the upward extension of the king's chamber northern shaft at the height of the apex of the pyramid. According to Cook, this requires an angle of 39.3° for the queen's chamber northern shaft. The ceilings of the queen's chamber shafts begin their angle of ascent 8.6 cubits horizontally from the midline of the pyramid. The king's chamber northern shaft intersects the height of the pyramid 297 cubits horizontally from the apex of the pyramid. The horizontal distance from the point the queen's chamber shaft begins its angle of ascent to the point the king's chamber shaft intersects the height of the apex of the pyramid is 288.4 cubits (297 minus 8.6). The vertical distance from the height of the ceiling of the queen's chamber shaft to the apex of the pyramid is 236 cubits (280 minus 44). The height of 236 cubits, times 11, divided by 9, equals 288.4 cubits.
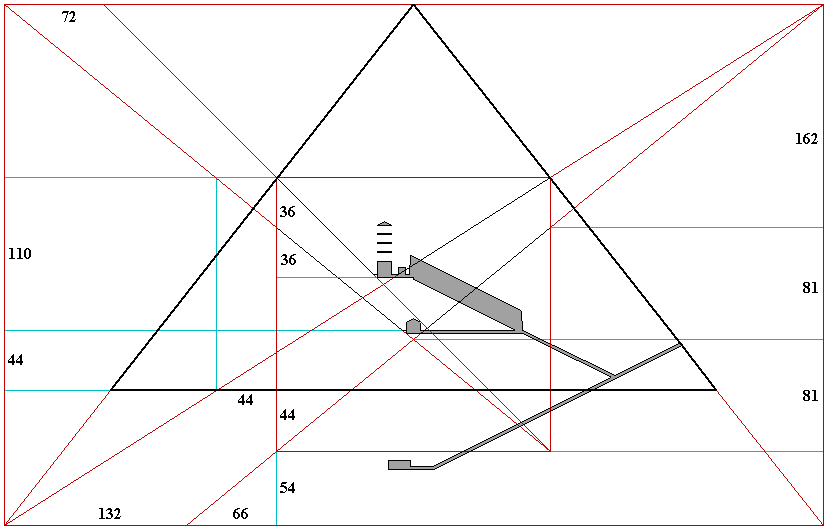
The sidelengths of the red square in the diagram are equal to the 198 cubit horizontal distance from the exit points of the king's chamber shafts. Extended downward, the king's chamber southern shaft marks the 280 cubit diagonal of the square, equal to the height of the pyramid. Cook suggested that the southern queen's chamber shaft, extended downward, also intersects the corner of the square. Given that the queen's chamber shafts are symmetrical, the queen's chamber northern shaft, extended downward, intersects the opposite lower corner of the square.
In the diagram above, the queen's chamber shafts terminate directly below the exit points of the king's chamber shafts, 118 cubits above ground level and 99 cubits horizontally from the midline of the pyramid. Given the height of 44 cubits for the shafts in the queen's chamber, the rise of the shafts is 74 cubits. The run of the ascending portion of the shafts is equal to the 99 cubit distance from the midline, minus the five cubit width of the chamber from the midline, and minus the 3.6 cubit horizontal run of the shafts from the chamber, or 90.4 cubits. A rise of 74 cubits over a run of 90.4 cubits produces a 116.8 cubit length for the ascending portion of the shafts. Adding the 3.6 cubit horizontal distance gives a total length of 120.4 cubits for the queen's chamber shafts. The distance of the shafts reported by Hawass is 208 feet, or approximately 121 cubits. Extended downward, the queen's chamber shafts intersect at the vertical midline of the pyramid. The shafts begin their angle of ascent 8.6 cubits horizontally away from the midline. 8.6 times 9/11 equals 7.0 cubits. Given the height of 44 cubits for the shafts at the walls of the queen's chamber, the intersection point is 37 cubits above ground level. From the upper end of the shafts to the intersection point at the midline of the pyramid the vertical distance is 81 cubits and the horizontal distance is 99 cubits.
The vertical distance from the floor of the king's chamber to the exit points of the king's chamber shafts is 72 cubits (154 minus 82). The 72 cubit vertical distance is divided in half by the upper ends of the queen's chamber shafts. Extended upwards, the queen's chamber southern shaft intersects the height of the pyramid 72 cubits south of the point the king's chamber southern shaft intersects the height of the pyramid.
The queen's chamber shafts begin 44 cubits above ground level, 110 cubits vertically below the exit point of the king's chamber shafts, equal to the 110 cubit horizontal distance of the king's chamber northern shaft. The vertical distance from the intersection point of the queen's chamber shafts to the termination of the queen's chamber shafts is 81 cubits, equal to one-half of the 162 cubit vertical distance from the termination of the queen's chamber shafts to the apex of the pyramid. The intersection point of the queen's chamber shafts is also 81 cubits above the lower edge of the 198 cubit square in the diagram. Extended downward, the queen's chamber northern shaft is 132 cubits horzonally from the intersection point of the south face of the pyramid and the king's chamber northern shaft, and one-half of this distance, or 66 cubits horizontally from the exit points of the king's chamber shafts.
ASTRONOMICAL ALIGNMENTS
Kate Spence proposed that the pyramid builders used the simultaneous transit of Kochab and Mizar, in vertical alignment above and below the north polar region, to orient the sides of the pyramid to the cardinal directions. In 2467 B.C. the vertical alignment of Kochab and Mizar was due north. As a result of precession, the vertical alignment of Kochab over Mizar slowly moved east of due north after 2467 B.C. The vertical alignment of Kochab over Mizar was west of due east, slowly moving east towards due north, prior to 2467 B.C. The great pyramid is oriented approximately three arc minutes west of due north. Kochab was vertically aligned over Mizar three arc minutes west of due north around 2480 B.C. One problem with Spence's theory is that the second pyramid at Giza is aligned approximately six arc minutes west of due north. Kochab was vertically over Mizar six minutes west of due north around 2486 B.C. This contradicts the conventional chronology that the second pyramid was built after the great pyramid. Spence explains this discrepancy by suggesting that the second pyramid could have been oriented by the simultaneous transit of Mizar over Kochab. In 2467 B.C. the vertical alignment of Kochab over Mizar and the vertical alignment of Mizar over Kochab were both due north. But as the vertical alignment of Kochab over Mizar moved east of due north after 2467, the vertical alignment of Mizar over Kochab moved west. The simultaneous transit of Mizar over Kochab, six minutes west of due north, occurred around 2448 B.C. This is Spence's proposed date for the orientation of the second pyramid.
Giuglio Magli argues that while Spence may be right about the date of the orientation of the great pyramid based on the simultaneous transit of Kochab over Mizar, the idea that the builders would have used opposite simultaneous transits for the first and second pyramid at Giza is unlikely. In the alternative, Magli suggests that the simultaneous transit of Kochab over Mizar was also used to orient the second pyramid, meaning that it would have been oriented first, around 2486 B.C.
A third alternative is that both pyramids were oriented by the simultaneous transit of Mizar over Kochab. In this case the date of the orientation of the great pyramid would be around 2454 B.C. and the date of the orientation of the second pyramid would have been around 2448 B.C., preserving the conventional chronology of the two pyramids and applying the same method of orientation for both pyramids.
Virginia Trimble and Alexander Badawy proposed that the southern king's chamber shaft targeted Orion's belt and that the northern king's chamber shaft targeted the area of the north celestial pole. Robert Bauval used Gantenbrink's data on the angles of the shafts to calculate the approximate dates that the southern king's chamber shaft targeted Orion's beltstar Alnitak and the northern shaft targeted Thuban, the closest star to the north pole during the pyramid age. Bauval also used Gantenbrink's estimates of the mean angles of the queen's chamber shafts to calculate the approximate dates that the southern shaft targeted Sirius, and the northern shaft targeted Kochab. However, Gantenbrink only measured the angle of less than half of the southern queen's chamber shaft and he was only able to penetrate the northern queen's chamber shaft to the bend around the grand gallery. The report of the more recent survey by Hawass, indicating that the total length of both of the queen's chamber shafts is the same, and that both shafts terminate at the same relative locations inside the pyramid, supports Gantenbrink's earlier speculation that the shafts were intended to be symmetrical.
Sources of error in dating the pyramid from calculations based on the surveyed angle of the shafts include: The ability of the ancient Egyptians to accurately measure the angles of the stars above the horizon at culmination; the ability of the ancient Egyptians to construct the shafts to accurately match their measure of the angles of the stars; and the ability of modern surveys to accurately determine the angles of the shafts. In addition to the 14/11 slope of the pyramid and the 1/2 slope of the entrance passage, the pyramid builders may have used the simple slopes of 1/1, 7/11 and 9/11, as close approximations to the angles of the culminations of the stars, in planning the locations of the chambers, passages and shafts, and in constructing the pyramid. If so, we can only guess at the precise angles that builders were approximating with the whole number slopes used in construction.
The queen's chamber shafts offer a simpler and more accurate method for astronomically dating the pyramid, if the northern queen's chamber shaft was intended to target Kochab and the southern queen's chamber shaft was intended to target Sirius, and if the queen's chamber shafts were intended to be symmetrical. Kochab is believed to have been an important star to the ancient Egyptians of the pyramid age. As Thuban was slowly moving away from the north celestial pole, Kochab was moving closer to the pole. If the proposals of Spence and others are correct that Kochab was used to orient the sides of the pyramids to the cardinal directions, this also indicates the importance of Kochab to the ancient Egyptians. Sirius is known to have been the most important star in the sky to the ancient Egyptians. Sirius is the brightest star in the sky and the ancient Egyptian calendar was based on the heliacal rising of Sirius. The heliacal rising of Sirius also signaled the beginning of the annual flooding of the Nile that the ancient Egyptian civilization depended upon.
During the pyramid age, Kochab was moving closer to the north celestial pole. As a result, the circle described by Kochab as it rotated around the pole was getting smaller and Kochab's upper culmination was getting lower in the northern sky. While the upper culmination of Kochab was getting lower in the northern sky, the culmination of Sirius was getting higher in the southern sky. In the sky above Giza, the upper culmination of Kochab was higher than the culmination of Sirius, prior to 2450 B.C. The culmination of Sirius was higher than the upper culmination of Kochab after 2450 B.C. The upper culmination of Kochab and the culmination of Sirius were the same angle above the horizon in the sky above Giza in 2450 B.C. Given the significance of Kochab and Sirius to the ancient Egyptians, it is likely that they were aware that the angles above the horizon of the culminations of Sirius and Kochab had been getting closer to each other for hundreds of years, and one of the purposes of the shafts may have been to memorialize the time when the culminations of both stars were at the same angle above the horizon. The angle of both stars above the horizon was approximately 39.35° in 2450 B.C. This is close to the angles proposed by Gantenbrink from his survey and close to the angle produced by the 9/11 slope proposed above. 2450 B.C. is also close to the astronomically derived orientation date given by Spence based on the simultaneous transit of Kochab over Mizar, and even closer to the astronomically derived orientation date if the great pyramid and the second pyramid at Giza were both oriented based on the simultaneous transit of Mizar over Kochab.
See Also: