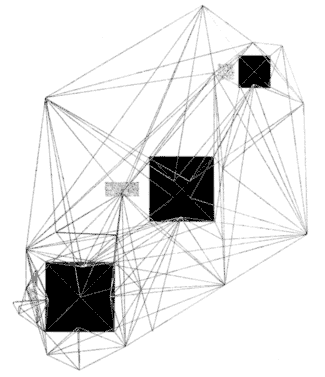
THE SITEPLAN OF THE GIZA PLATEAU

Below is an illustration of WMF Petrie's survey by triangulation of the three major pyramids at Giza:

The results of Petrie's survey by triangulation, in inches, are as follows:

  NS Distance: EW Distance: Total Distance (angle west of due south):
Centre of First to centre of Second Pyramid 13931.6 13165.8 19168.4 at 43º 22' 52"
Centre of First to centre of Third Pyramid 29102.0 22616.0 36857.7 at 37º 51' 6"
Centre of Second to centre of Third Pyramid 15170.4 9450.2 17873.2 at 31º 55' 12"

These measurements convert to cubits as follows:

  NS Distance: EW Distance: Total Distance

Centre of First to centre of Second Pyramid

 675.6 638.5 929.6
Centre of First to centre of Third Pyramid 1411.3 1096.8 1787.5
Centre of Second to centre of Third Pyramid 735.7 458.3 866.8

Petrie's measurements of the base lengths of the pyramids at Giza are as follows:

  Inches Cubits
First Pyramid 9,068.8 440
Second Pyramid 8,474.9 411
Third Pyramid 4,153.6 201.5

Petrie's measurements of the heights of the pyramids at Giza are as follows:

  Inches Cubits
First Pyramid 5776 280
Second Pyramid 5664 274.5
Third Pyramid 2580 125
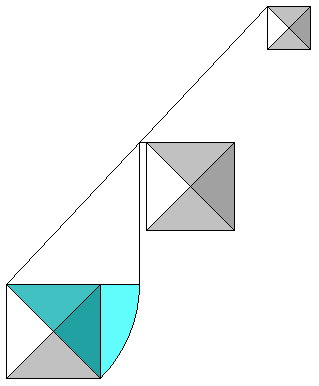
Based on Petrie's measurements, John Legon diagrammed the relative positions of the three main pyramids at Giza as follows:

Mark Lehner found evidence of a diagonal survey line running from the SE corner of the first pyramid to the SE corner of the third pyramid. The EW distance between the SE corner of the first pyramid and the SE corner of the third pyramid is 1,216 cubits and the NS distance is 1,292 cubits. The slope of the hypotenuse of this right triangle is 16/17. The units of this fraction are 76 cubits long. 76 cubits times two is also the 152 cubit distance from the western edge of the second pyramid to the eastern edge of the third pyramid.

The distance from the southern edge of the first pyramid to the southern edge of the second pyramid is 661 cubits. At the southern edge of the second pyramid, the Lehner diagonal is 622 cubits west of the eastern edge of the first pyramid:

661 x 1216 ÷ 1292 = 622

622 cubits is also the length of the diagonal baselength of the first pyramid:

440 x √2 = 622

The diagonal of the first pyramid arced to the southern edge of the first pyramid and a line drawn due south from this point to the Lehner diagonal marks the southern edge of the second pyramid.

The Lehner diagonal passes the southern edge of the second pyramid 31 cubits east of the eastern edge of the second pyramid (653 - 622 = 31). The baselength of the first pyramid is 29 cubits longer than the baselength of the second pyramid (440 - 411 = 29). Thus, a diagonal line from the SW corner of the first pyramid to the SW corner of the second pyramid is very nearly parallel to the diagonal from the SE corner of the first pyramid to the SE corner of the third pyramid

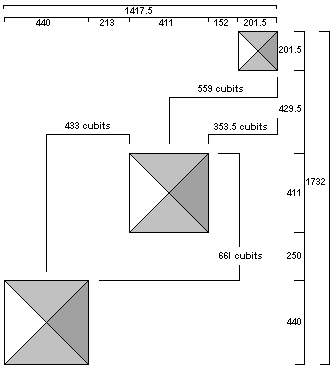
The NS distance between the southern edge of the first pyramid and the northern edge of the second pyramid is 250 cubits. Legon observed that in addition to the 250 cubit NS spacing between the first two pyramids, other measures are also based on 250 cubits multiplied by elementary square roots.

The square root of two is 1.414. The EW distance from the western edge of the second pyramid to the western edge of the third pyramid is 353.5 cubits:

250 x 1.414 = 353.5

The square root of three is 1.732. The EW distance from the center of the first pyramid to the eastern edge of the second pyramid is 433 cubits:

250 x 1.732 = 433

The square root of five is 2.236. The EW distance from the center of the second pyramid to the western edge of the third pyramid is 559 cubits:

250 x 2.236 = 559

The square root of seven is 2.646. The NS distance from the southern edge of the first pyramid to the southern edge of the second pyramid is 661 cubits:

250 x 2.646 = 661

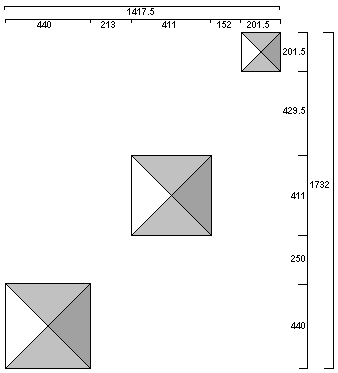
The combined height of the pyramids is 280 + 274.5 + 125 = 679.5 cubits. This is equal to the two NS spaces between the three pyramids (250 + 429.5 = 679.5). The combined baselength of the pyramids is 440 + 411 + 201.5 = 1052.5 cubits. The combined height and baselength of the pyramids is 679.5 + 1052.5 = 1732 cubits.

The sum of the two EW spaces (213 + 152) is 365 cubits, equal to the number of days in a year. The circumference of a circle with a diameter equal to the diagonal baselength of the second pyramid is equal to the number of days in a year times five:

411 x √2 = 581.24

581.24 x π = 1826

1826/5 = 365

The distance from the apex of the first pyramid to the apex of the third pyramid is 36,857.7 inches. This is the hypotenuse of the right triangle formed by the NS distance and the EW distance from apex to apex. The slope of this diagonal west of due south may be expressed as the fraction: 22,616/29,102. This reduces to almost exactly 7/9. The angle of the apexes of the first and third pyramids west of due south is 37° 51' 6". A true7/9 right triangle has an angle of 37° 52' 30''. The margin of error is just over one arc minute, or approximately 20 inches over a distance of 36,857.7 inches:

22,616 inches x 9 ÷ 7 = 29,078 inches

29,102 inches x 7 ÷ 9 = 22,634 inches

In cubits, the margin of error is within one cubit, over a distance of 1,787 cubits:

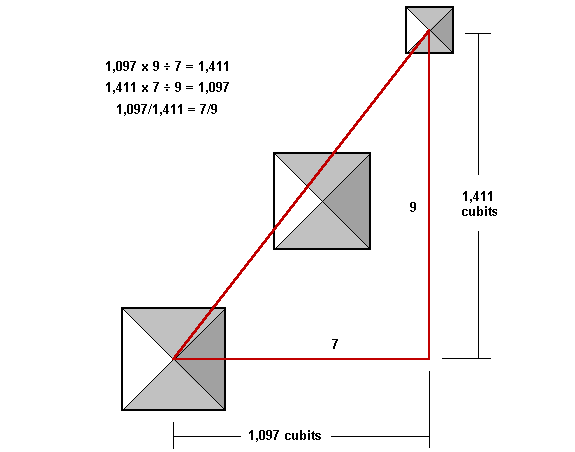
The difference between the 1,411 cubit NS distance and the 1,087 cubit EW distance between the apexes of the pyramids is also a good approximation of π x 100:

1,411 - 1,097 = 314

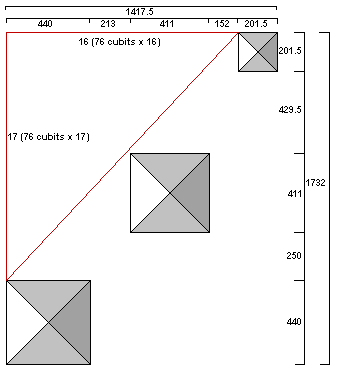
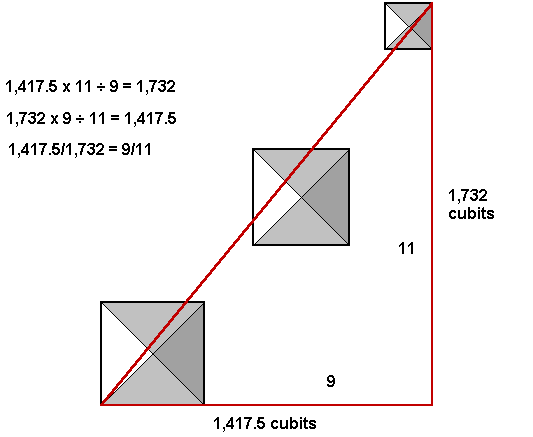
The longest distance between the three major pyramids at Giza is from the NE corner of the first pyramid to the SW corner of the third pyramid. The baselength of the third pyramid is 201.5 cubits. The EW distance from the apex of the first pyramid to the apex of the third pyramid is 1096.8 cubits and the NS distance is 1411.3 cubits. To calculate the distance from the NE corner of the first pyramid to the SW corner of the third pyramid, one half of the baselength of both pyramids is added to the measurements from the apexes:

1096.8 + 220 + 100.75 = 1,417.5 cubits EW.

1411.3 + 220 + 100.75 = 1,732 cubits NS.

The slope of the diagonal from the NE corner of the first pyramid to the SW corner of the third pyramid is 1.417.5/1,732. Robin Cook observed that this reduces to a slope of 9/11. The angle west of due south from the NE corner of the first pyramid to the SW corner of the second pyramid is 39° 17' 51". A true 9/11 right triangle has an angle of 39° 17' 22". The margin of error is less than 30 arc seconds:

The distance from the eastern edge of the first pyramid to the western edge of the third pyramid is 1417.5 cubits and the NS distance from the apex of the first pyramid to the apex of the third pyramid is 1411 cubits. The hypotenuse of this right triangle is the NS midpoint of the first pyramid on the east side and the NS midpoint of the third pyramid on the west side. The distance of the hypotenuse is 2000 cubits.

Robin Cook observed that the distance from the NE corner of the first pyramid to the SW corner of the second pyramid is equal to the NS distance from the northern edge of the first pyramid to the northern edge of the third pyramid. Clive Ross observed that the distance from the SW corner of the third pyramid to the NE corner of the second pyramid is equal to the NS distance from the southern edge of the third pyramid to the southern edge of the first pyramid. These relationships are shown in the diagram below. The rectangle in the diagram below that is formed by the SE corner of the first pyramid and the NW corner of the third pyramid has an EW distance of 1417.5 cubits and a NS distance of 1090.5 cubits. This reduces to a ratio of 13/10:

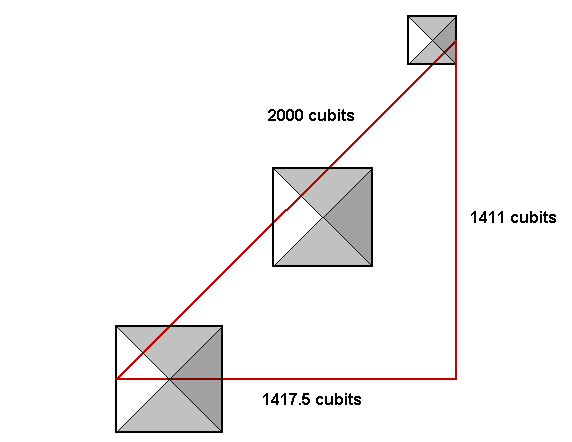
1417.5/1090.5 = 13/10.

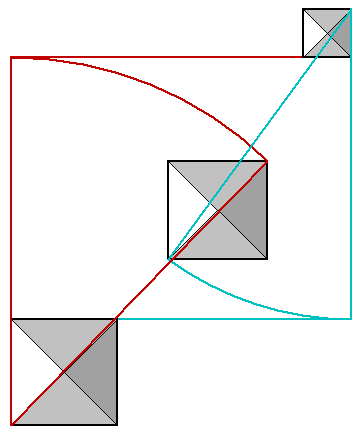
The distance from the SW corner of the third pyramid to the NE corner of the second pyramid is 1292 cubits. The distance from the SW corner of the the third pyramid to the NE corner of the first pyramid is 2238 cubits. Ross also observed that 2238/1292 = 1.732.

Robin Cook observed that the distance from the apex of the first pyramid to the NE corner of the second pyramid is equal to the EW distance from the midline of the first pyramid to the midline of the second pyramid. The distance from the NW corner of the third pyramid to the SW corner of the second pyramid is also very nearly the same as the EW distance from the west side of the third pyramid to the midline of the second pyramid.

Cook measured the distances between the apexes and the corners of the pyramids along 45° diagonals to the cardinal directions and found that the diagonal distance from the SW corner of the third pyramid to the NE corner of the second pyramid is in the ratio of two to one to the diagonal distance from the NE corner of the second pyramid to the apex of the first pyramid. Cook also found that the diagonal distance from the apex of the first pyramid to the apex of the second pyramid is in the ratio of 11/10 to the distance from the apex of the second pyramid to the apex of the third pyramid. The diagonal box shown below that is bounded by the southern corners of the third pyramid and the northern corners of the first pyramid is also bisected by the diagonal of the second pyramid and the distance between the apexes of the first and third pyramids is in the ratio of 21/8 to the sidelength of this bounding box.

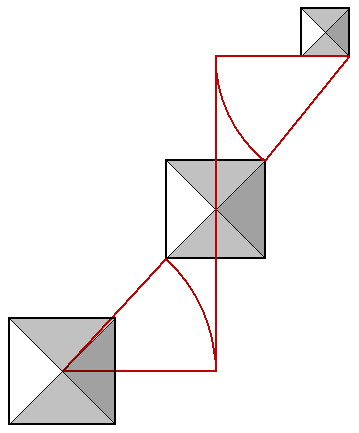
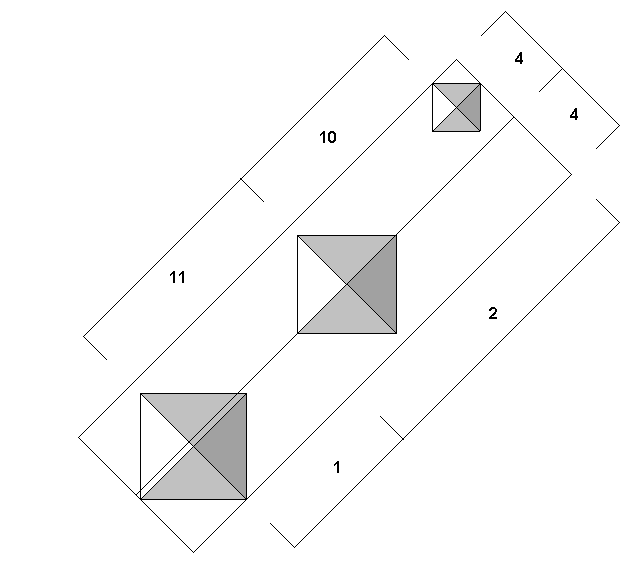
A 45° diagonal from the apex of the third pyramid intersects the SE diagonal of the first pyramid very nearly 220 cubits from the apex of the first pyramid. Thus, a circle inscribed inside the first pyramid very nearly marks the point on the SE diagonal of the first pyramid that is at a 45° angle to the apex of the third pyramid. This 45° diagonal line from the SE diagonal of the first pyramid to the apex of the third pyramid is divided by the SE diagonal of the second pyramid in the ratio of 11/10, as shown in the diagaram above. The length of this diagonal is 1773 cubits, a close approximation of the square root of π x 1000. The EW distance between the apex of the first pyramid and the apex of the third pyramid divides the 45° diagonal into golden sections.

Chris Tedder proposed a site plan for the Giza Pyramids based on golden sections. A 45° diagonal line is extended for 2000 cubits from the mid point of the eastern edge of the great pyramid. The red square formed by this diagonal has side lengths of 1414 cubits. A line is drawn from the southern edge of the great pyramid at the mid point of the western half of the pyramid, to the mid point of the western edge. This line is arced to the level of the southern edge of the pyramid. The mid point of the western face of the pyramid and the point where the arc intersects the extended southern edge of the pyramid form a golden section rectangle. The NS side length is 220 cubits and the EW side length is 136 cubits (220/1.618 = 136). The diagonal of this rectangle is extended to the southern edge of the red square (this point marks the apex of the third pyramid). The NS distance of this line is 1414 cubits and the EW distance is 874 cubits (1414/1.618 = 874). The line from the western face of the great pyramid begins 440 cubits west of the eastern edge of the red square. 440 + 874 = 1314. Thus, the apex of the third pyramid is 100 cubits east of the western edge of the red square, giving 200 cubits for the side lengths of the third pyramid.

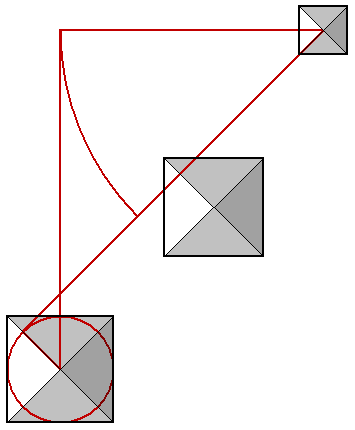
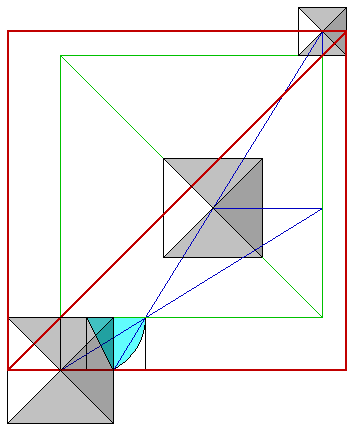
A smaller square is drawn from the mid point of the southern edge of the great pyramid and the mid point of the northern edge of the third pyramid. Another golden section rectangle is formed by the apex of the great pyramid and the point where the arc intersects the level of the southern edge of the pyramid. The EW side length of this rectangle is 356 cubits (220 + 136 = 356) and the NS side length is 220 cubits (356/1.618 = 220). The diagonal of this rectangle is extended to the NS green line from the mid point of the northern edge of the third pyramid. The EW distance of this diagonal is 1094 cubits (1414 - 220 - 100 = 1094). The NS distance of this diagonal is 676 cubits (1094/1.618 = 676). The SE and NW diagonal of the second pyramid is aligned with the diagonal of the green square. The diagonal from the mid point of the western edge of the great pyramid to the apex of the third pyramid intersects the diagonal of the green square at the apex of the second pyramid. The diagonal from the apex of the great pyramid also intersects the NS green line from the third pyramid at the same NS level as the apex of the second pyramid, 676 cubits south of the apex of the great pyramid.

The NS distance from the apex of the first pyramid to the second pyramid and the EW distance from the apex of the first pyramid to the third pyramid forms a golden section rectangle. The NS distance from the apex of the second pyramid to the apex of the third pyramid and the EW distance from the apex of the second pyramid to the apex of the third pyramid also forms a golden section rectangle:

EW P1 - P3/NS P1 - P2 = 1.618

NS P2 - P3/EW P2 - P3 = 1.618

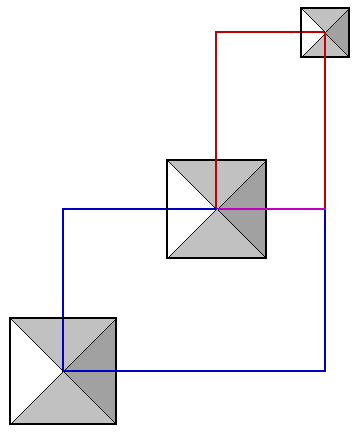
The diagonal baselength of the first pyramid is 622 cubits (440 x √2 = 622). 1/8th of the baselength of the first pyramid is 55 cubits (440/8 = 55). Extending the diagonal of the first pyramid to the SE by 1/8th of the baselength of the first pyramid gives a diagonal length of 677 cubits (the short side of the diagonal bounding box below). The long side of the diagonal bounding box in the diagram is 677 x φ² = 1772.4 cubits. 1772.4 is the square root of π x 1000. The corner of the diagonal bounding box at the SE corner of the third pyramid is 1732 cubits south and 1214 cubits west of the NE corner of the first pyramid. The south edge of the third pyramid is 1732 cubits south of the north edge of the first pyramid and with a baselength of 200 cubits, the west edge of the third pyramid is 1414 cubits west of the east edge of the first pyramid.

Each of the three main pyramids at Giza had a temple adjoining it and at the end of a causeway each of the pyramids had another temple, commonly referred to as the valley temples. The temple directly in front of the sphinx and right next to the second pyramid's valley temple is known as the sphinx temple. The EW distance from the western edge of the third pyramid to the eastern edge of the second pyramid's valley temple and the sphinx temple is 2,000 cubits. The distance from the northern edge of the first pyramid to the southern edge of the third pyramid is 1,732 cubits. 1,732 is equal to the square root of three times 1,000. 2,000 is equal to the square root of four times 1,000. The diagonal of this rectangle is 2,645.75 cubits long. 2,645.75 is equal to the square root of seven times 1,000. This expresses Pythagoras theory in the form of:

√3² + √4² = √7²

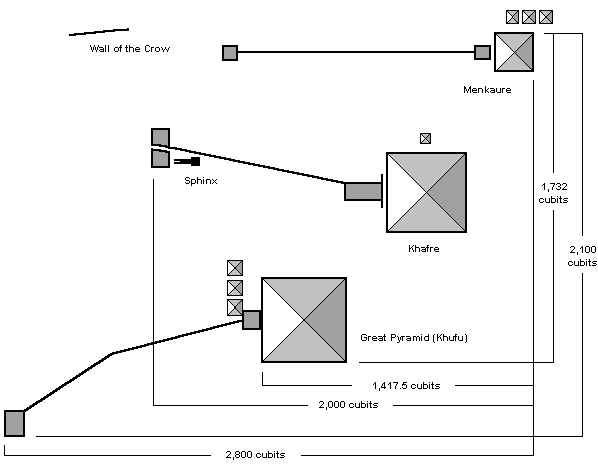
The NS distance from the southern edge of Menkaure to the northern edge of Khufu's valley temple is 2,100 cubits. The EW distance from the western edge of Menkaure to the eastern edge of Khufu's valley temple is 2,800 cubits. The diagonal of the rectangle described by the SW corner of Menkaure and the NE corner of Khufu's valley temple is 3,500 cubits long, demonstrating a 3-4-5 right triangle of 2,100 - 2,800 - 3,500 cubits.

See Also:

Geometric construction of the Giza siteplan

Proposed Giza siteplan

Giza siteplan: Squaring the circle

Dashur siteplan

Bent Pyramid Geometry

Survey diagrams of the Giza Plateau by:

Mark Lehner

David Ritchie

BACK