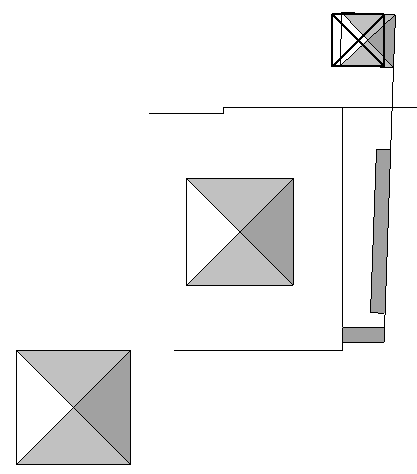
SQUARING THE CIRCLE: SITEPLAN OF THE THREE MAIN PYRAMIDS AT GIZA
The problem of geometrically constructing a square with an area equal to the area of a circle is the problem of geometrically constructing a line with a length equal to the square root of pi, because a square with sidelengths equal to the square root of pi has an area equal to the area of a circle with a radius of one. The following equation provides a very accurate solution to this problem. This same solution is also demonstrated geometrically by the siteplan of the three main pyramids at Giza.
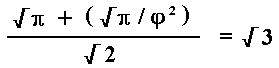
The square root of pi is 1.77245...
Phi squared is 2.61803...
The square root of pi divided by phi squared is .67702...
1.77245... + .67702... = 2.44947...
2.44947... divided by the square root of two (1.41421...) = 1.73204...
The square root of three is 1.73205...
This equation may be restated as follows:
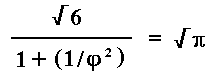
The square root of six is 2.44949...
One divided by phi squared is .38197
1 + .38197... = 1.38197...
2.44949... divided by 1.38197... = 1.77246...

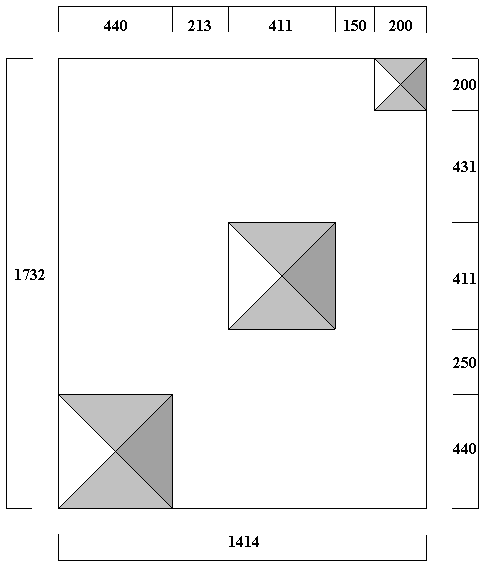
The given equations are shown by the Giza pyramids as follows. The scale of the diagram above: One equals 1000 cubits. The south side of the third pyramid is 1732 cubits south of the north side of the great pyramid and the west side of the third pyramid is 1414.2 cubits west of the east side of the great pyramid. The 1732 cubit north-south distance is in precise accord with W.M.F. Petrie's survey of Giza. The 1414.2 cubit east-west distance is in approximate accord with survey results, leading to the conclusion by some researchers that the overall north-south and east-west dimensions of the site were intended to be√3 x 1000 and √2 x 1000. The diagonal baselength of the great pyramid is 622.04 cubits, or 439.85 cubits for the east-west and north-south baselengths. This is in close accord with Petrie's measure of 9068.8 inches for the baselength and his value of 20.62 inches for the length of the cubit used to construct the great pyramid, derived from various measures of the interior and exterior of the pyramid. The baselength of the third pyramid is 199.78 cubits. As a result of it's unfinished and deteriorated condition, survey results for the baselength of the third pyramid vary from approximately 195 to 205 cubits. The most common estimate of the intended size of the third pyramid is 200 cubits. Petrie's measure of the baselengths of the third pyramid equate to 201.5 cubits, based on the great pyramid cubit of 20.62 inches, but Petrie believed that a slightly longer cubit was used to construct the third pyramid and that the intended baselength was 200 cubits.
One eighth of the baselength of the great pyramid is 54.98 cubits. Extending the southeast diagonal of the great pyramid (622.04 cubits) by one eighth of the NS baselength produces a 677.02 cubit diagonal (√π x 1000/φ²). Extending a perpendicular line from the end point of this diagonal for a distance equal to the length of the diagonal times phi squared (677.02 x φ² = 1772.45) marks the southeast corner of the third pyramid. The north-south distance from the north side of the great pyramid to the south side of the third pyramid is equal to the two diagonals, 677.02 cubits plus 1772.45 cubits, divided by the square root of two, equals 1732.04 cubits. The east-west distance from the west side of the great pyramid to the east side of the third pyramid is equal to 1772.45 cubits minus 677.02 cubits, divided by the square root of two, equals 774.58 cubits. Adding the baselength of the great pyramid gives the east-west distance from the east side of the great pyramid to the east side of the third pyramid (774.58 + 439.85 = 1214.43). Adding the baselength of the third pyramid gives the east-west distance from the east side of the great pyramid to the west side of the third pyramid (1214.43 + 199.78 = 1414.21).
In the alternative, the sizes and locations of the Giza pyramids may be shown by geometric construction of the given equations as follows: Construct a 45° diagonal line of any length, rising from right to left (segment AB). Construct a perpendicular line from point B, extended for a distance equal to the length of segment AB times phi squared as follows: Arc BA to point F. Arc FB to point G. Construct a perpendicular line from point F to point H. Construct the midpoint of FG at point I. Arc IH to point C. Segment BC is equal to segment AB times phi squared. Construct perpendicular lines from point A and point C to point D, producing the rectangle ABCD. Construct the midpoint of segment CD and bisect rectangle ABCD with a perpendicular line from point E.
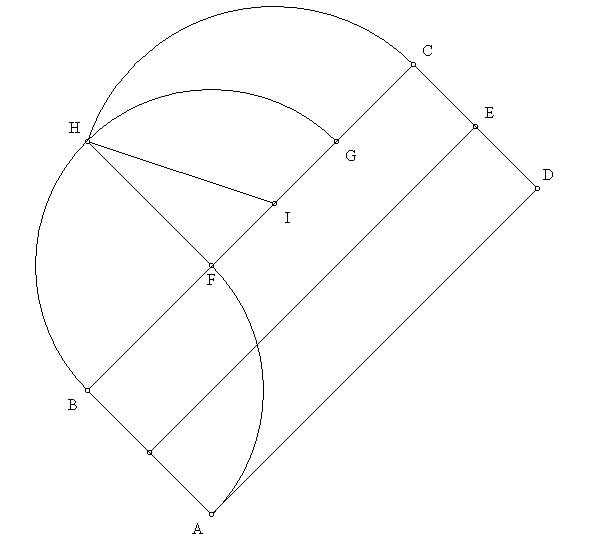
The length of BC is equal to the length of AB times phi squared. The vertical distance from point A to point C is equal to the length of AB plus the length of BC, divided by the square root of two. If AB is assigned a length of the square root of pi divided by phi squared, then BC is equal to the square root of pi, and the vertical distance from point A to point C is equal to the square root of three. Extend horizontal lines from point A and point C. Mark the midpoint of the horizontal distance between point B and point E at point F. From the vertical distance that equals the square root of three, construct a segment equal to one, and from the segment equal to one, construct a segment equal to the square root of two (not shown). Center the square root of two segment (GH) on point F. Draw rectangle GHIJ. Segments GJ and HI are equal to the square root of three. Segments GH and IJ are equal to the square root of two. Mark points K and L where rectangle ABCD intersects rectangle GHIJ. Segments BK and EL are of equal length. The diagonal segment AK is shorter than the short side of the diagonal rectangle by the same distance that the diagonal CL is shorter than one-half of the short side of the diagonal rectangle.
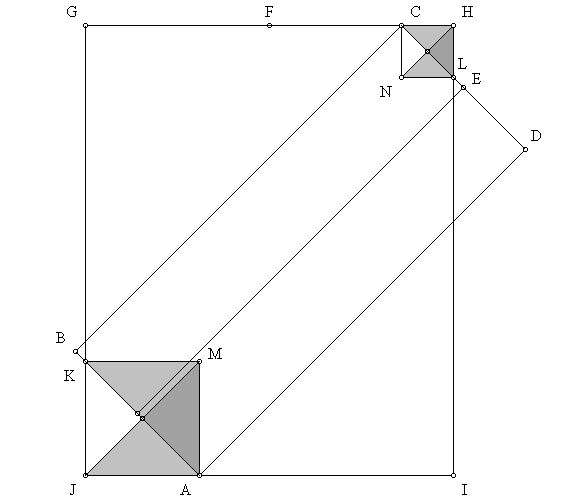
The corners of the great pyramid are marked by points A, J, K and M. The corners of the third pyramid are marked by points C, H, L and N. Given a scale of one equals 1000 cubits, the sidelengths of the great pyramid measure 439.5 cubits. This is the only measure of the sidelengths of the great pyramid that is possible when the short side of the diagonal rectangle (AB), and one-half of the opposite short side of the diagonal rectangle (CE) are projected an equal distance beyond the √3-√2 rectangle. When Petrie surveyed the dimensions of the great pyramid, he believed that the exact dimensions of the king's chamber gave the best evidence of the length of the cubit used to construct the pyramid. The length of the cubit used to construct the king's chamber measured 20.632 inches. One reason that Petrie concluded that the cubit used to construct the great pyramid was slightly shorter than the length of the cubit he found in the king's chamber is because of the assumption that the baselength of the pyramid was intended to be an even 440 cubits. Petrie's 9068.8 inch measure for the base length of the great pyramid, divided by the king's chamber cubit of 20.632 inches, produces a baselength for the great pyramid of 439.5 cubits. This is the precise value for the baselength of the great pyramid that is produced by the geometric construction above. The sidelength of the third pyramid that is produced by the construction above is 200.1 cubits.
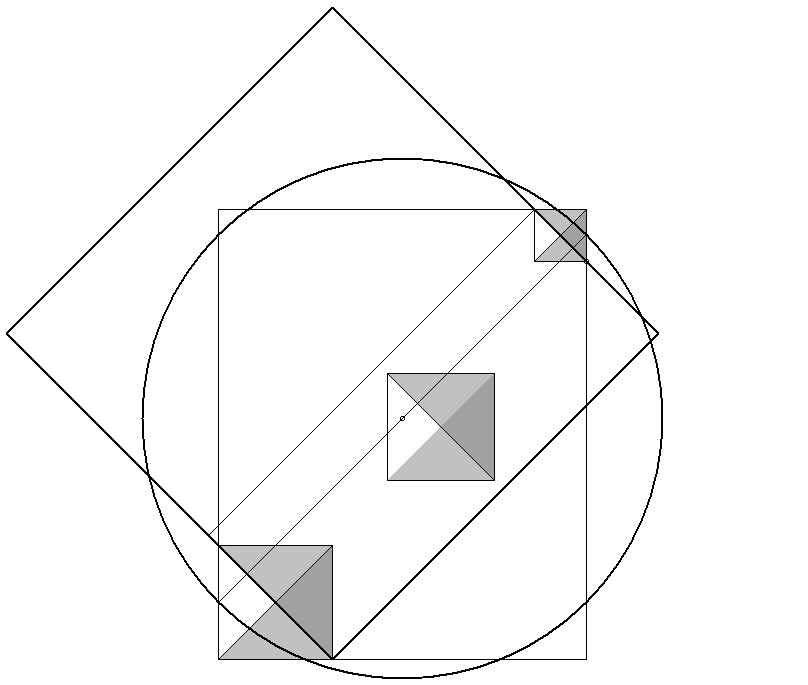
The 45° diagonal distance from the east side of the great pyramid to the west side of the third pyramid is 2000 cubits. The radius of the circle is 1000 cubits and the area of the circle is 3,141,593 cubits. The sides of the square are 1772.45 cubits long. The area of the square is also 3,141,593 cubits.
The consructions above produce the sizes and relative locations for the first and third pyramids as shown below in even numbers of cubits. The size and location of the second pyramid is shown in relation to the first pyramid according to Petrie's survey.
The north-south distance from the south side of the great pyramid to the north side of the second pyramid is 250 cubits. Given a scale of one equals 1000 cubits, 250 cubits is 1/4. The east west distance from the apex of the third pyramid to the west side of the second pyramid is also 250 cubits. The distance from the south side of the great pyramid to the south side of the second pyramid is 661 cubits. The square root of seven is 2.64575. The square root of seven divided by four is .66143. The distance from the apex of the third pyramid to the east side of the second pyramid is also 661 cubits. These one over four and square root of seven over four ratios mark all four sides of the second pyramid. The square root of three is 1.73205. The square root of three divided by four is .43301 The east-west distance of the square root of three over four, from the apex of the great pyramid, also marks the east side of the second pyramid.
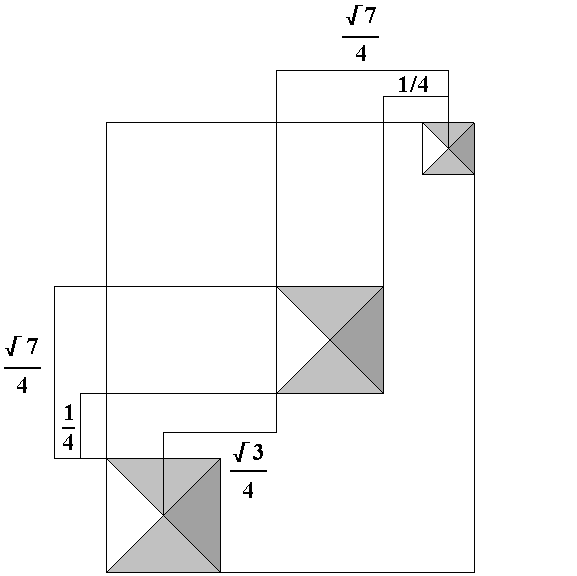
The marking of the location of the east side of the second pyramid from the apex of the great pyramid and the apex of the third pyramid provides a check on the accuracy of the geometric construction. Given the sizes of the pyramids produced by the geometric construction, the east-west distance from the east side of the great pyramid to the apex of the great pyramid is 219.75 cubits (439.5/2). The east-west distance from the west side of the third pyramid to the apex of the third pyramid is 100.05 cubits (200.1/2):
219.75 + 433.01 + 661.43 + 100.05 = 1414.24 cubits
The square root of two is 1.41421
PYRAMID ALIGNMENTS WITH THE CARDINAL DIRECTIONS
Petrie measured the orientation of the Giza pyramids as follows:
Great Pyramid, casing sides – 3' 43" ±
6"
Great Pyramid, core sides – 5' 16" ± 10"
Second Pyramid, casing sides– 5' 26" ±
16"
Second Pyramid, passage (Smyth) – 5' 37" ± 10" ?
Great Pyramid, passage (Smyth) – 5' 49" ± 7"
Third Pyramid, unfinished casing sides + 14' 3"
The average deviation of the first two pyramids is approximately five arc minutes, or less than one-tenth of one degree, west of due north. The deviation of the third pyramid is less than one-quarter of one degree east of due north, or west of due south. These minute discrepancies make it apparent that all three of the pyramids were intended to have the same orientation, in alignment with the cardinal directions.
The diagram below shows the pyramids, the workmans barracks, the peribolus walls of the second pyramid and the north peribolus wall of the third pyramid. Petrie measured a north-south distance of 5166 inches, or 250 cubits, from the outside of the second pyramid's south peribolus wall (east of the elbow joint) to the south-east corner of the second pyramid. Petrie stated that the north peribolus was the same distance from the second pyramid as the south peribolus. These measures equate with the 250 cubit measures above for the north-south distance from the south side of the great pyramid to the north side of the second pyramid and the east-west distance from the west side of the second pyramid to the apex of the third pyramid. Petrie also observed that the west wall of the workmans barracks, projected south, crossed 29 inches inside the west side of the third pyramid, leading Petrie to conclude that the west side of the third pyramid was intended to be aligned with the west side of the workman's barracks. The orientation of the west wall of the workmans barrack is 9' west of due south. In the diagram below, the pyramids, the peribolus walls and the workmans barracks are shown with the same orientation.

Petrie inclined his survey of the north-south and east-west distances between the pyramids by five minutes west of due north. Because the error of orientation of the third pyramid was to the east of due north while the error of orientation of the first two pyramids was to the west of due north, and because Petrie regarded construction of the third pyramid to be inferior to the first two pyramids, he disregarded the orientation of the third pyramid in orienting his survey. Petrie's measure of the north-south distance from the north side of the great pyramid to the south side of the third pyramid was 1732 cubits, in precise accord with the theoretical north-south measure in the geometric constructions above. Petrie's measure of the east-west distance from the east side of the great pyramid to the west side of the third pyramid was 1417.5 cubits, placing the west side of the third pyramid three cubits west of the 1414.2 cubit theoretical east-west measure in the geometric constructions above. In the diagram below, the different orientation of the workmans barracks and the third pyramid are greatly exaggerated. If the builders of the third pyramid measured south from the workmans barracks to locate the third pyramid and if they used the west of due south orientation of the workers barracks and of the third pyramid itself, the different orientation would have had no measurable effect on the north-south distance of the third pyramid from the other two pyramids, but it would have caused the third pyramid to be located further west than if the angle of orientation of the first two pyramids had been used to draw the line south to the location of the third pyramid. Adjusting Petrie's surveyed east-west distance from the east side of the great pyramid to the west side of the third pyramid to compensate for the deviation in the orientation of the third pyramid brings the east-west distance in line with the 1414.2 cubit distance in the geometric constructions above.