HEPTAGRAM CONSTRUCTION
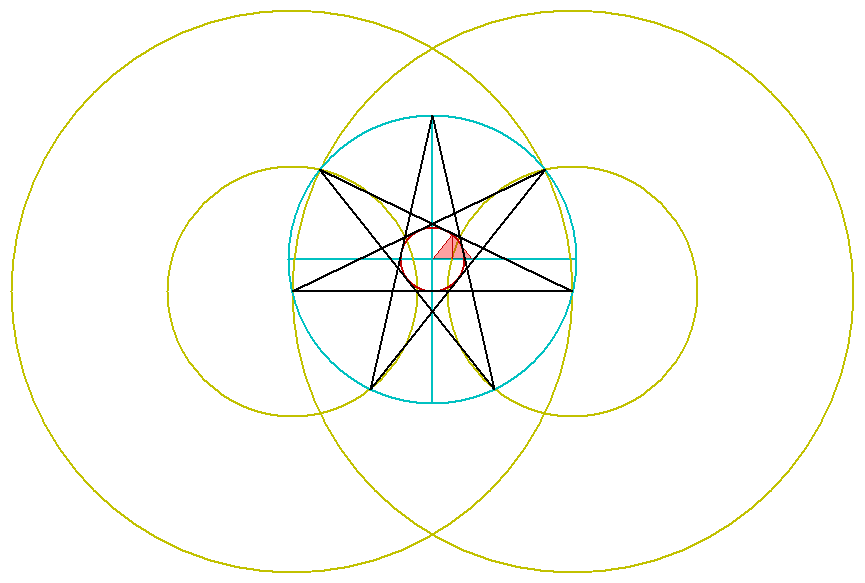
It is supposedly impossible to construct an exact heptagram with only a ruler and a compass. Below is a virtually perfect heptagram construction based on the dimensions of the great pyramid.

Draw a circle with center at point A. Construct a vertical and horizontal axis. Mark point B at the intersection point of the vertical axis and the edge of the circle. Draw circle BA. Repeat this process until 11 segments equal in length to segment AB are constructed. Segment AC is seven times the length of segment AB. Construct a horizontal line through point C. Segment AD is 10 times the length of segment AB. Construct circle AD. Segment AE is 11 times the length of segment AB. Arc segment AE down to the point where it intersects the right horizontal axis (point F). Construct the midpoint of segment AF (point G). Draw a perpendicular line from point G, intersecting horizontal line C at point H. With a baselength of 11 and a height of 7, the angular dimensions of triangle AHF are the same as the great pyramid. Construct the midpoint of segment AH (point I). Construct the midpoint of segment AI (point J). The dark shaded triangle has the same angular dimensions as the larger triangle and the great pyramid. Arc segment AJ to the point where it intersects the lower vertical axis (point K). Construct a horizontal segment from point K, intersecting the large circle at points 3 and 6.

Having fixed the distance of the horizontal segment from the center of the circle through the above operation, construct a vesica pisces with points 3 and 6 as the centers of the large outer circles. Mark the points where these circles intersect the central circle (points 2 and 7). Construct a circle with a radius from point 3 to point 2. Construct a circle with a radius from point 6 to the point 7. Mark the two lower points where the smaller circles intersect the central circle (points 4 and 5). The first point of the heptagram is point D from the diagram above, where the vertical axis intersects the top of the central circle.
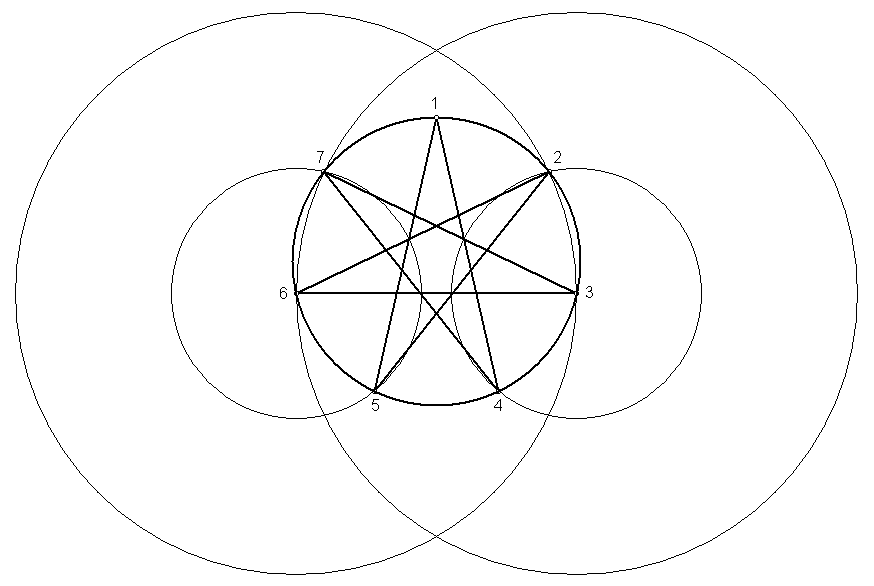
The acute angles at the points of an exact heptagram are 25° 42' 51" (180°/7). The acute angles formed by the construction above range from 25° 42' 14" to 25° 43' 05". Given a diameter of 20 for the circle around the heptagram, the length of each arm of a perfect heptagram is 18.019. The segments formed by the construction above range from 18.018 to 18.021.
Given a height of 280 cubits and a baselength of 440 cubits (7/11), the base angles of the great pyramid are 51° 50' 34". The ratio between the height of 7 and the half base of 5.5 is 1.272727. Beginning with an exact heptagram and performing the operation described above in reverse produces the following dimensions for the pyramid triangle. If segment AK is arced to the point it crosses the vertical axis of point J in the diagram above, the ratio between the height and the half base of the resultant triangle is 1.272401. This produces a base angle of 51° 50' 08". Given a baselength of 440 cubits, this base angle produces a height of 279.928 cubits. If segment AK is arced to the point it crosses the horizontal axis of point J in the diagram above, the ratio between the height and the half base of the resultant triangle is 1.273255. This produces a base angle of 51° 51' 15". Given a height of 280 cubits, this base angle produces a baselength of 439.817 cubits.