
The ancient Egyptian cubit of 20.62 ± .005 inches was used to build the great pyramid. The cubit was divided into seven palms of four digits each, or 28 digits per cubit. The base length of the pyramid at ground level is 440 cubits. Although the capstone has been missing since antiquity, the height of the completed pyramid, calculated from the base length and the slope of the faces, is 280 cubits. The slant height is 356 cubits (280² + 220² = 356²).
The Histories by Herodotus (440 B.C.) is one of the earliest surviving statements of the dimensions of the great pyramid. Herodotus reported that “the sides of the great pyramid are 8 plethra and the height is the same.” In ancient Greece, plethra denoted both a linear measure of 100 Greek feet and a square measure of one acre (100 × 100 feet). The linear measures of the sides and the height of the pyramid are not the same and they are not 800 feet or 800 cubits. The area of the 280 cubit height of the pyramid squared is 78,400 square cubits. The area of each side of the pyramid is equal to the slant height of the pyramid times one half of the base length. An area of 78,400 square cubits divided by 220 (one half of the base length) equals 356 (the slant height). 78,400 cubits divided by 8 equals 9800 cubits and the square root of 9800 is 99 cubits. The statement that the sides and the height of the pyramid are 8 plethra is based on an ancient Egyptian acre with side lengths of 99 cubits. The 99 cubit side lengths of the acre allowed ancient Egyptians to halve and double the acre with side lengths in whole numbers. One half acre is 4900 square cubits (side lengths of 70 cubits). Two acres is 19,600 square cubits (side lengths of 140 cubits). Four acres is 39,200 square cubits (side lengths of 198 cubits).
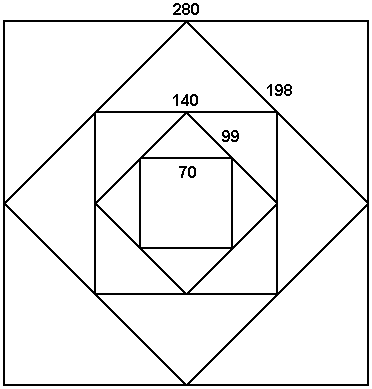
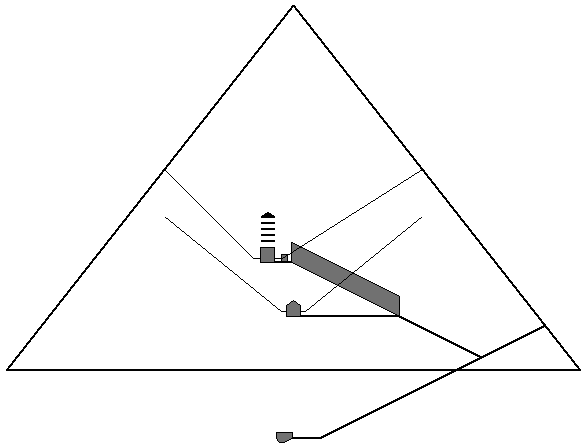
The floor of the king's chamber is 82 cubits above ground level or 198 cubits below the apex of the pyramid. A height of 198 cubits produces a square with an area of four ancient Egyptian acres. The area of the sides of the pyramid from the height of the king's chamber to the apex of the pyramid is also four acres. The king's chamber shafts exit the pyramid 154 cubits above ground level or 126 cubits below the apex of the pyramid. the side length of the pyramid at this height is 198 cubits. The horizontal area of the pyramid at this height is also four acres. The king's chamber shafts begin their angles of ascent two cubits above the floor of the king's chamber or 84 cubits above ground level. The angle of the southern shaft is 45°. The rise/run of this shaft is 1/1. The rise of the shaft is 70 cubits (154 - 84 = 70) and the run of the shaft from the point it begins it's angle of ascent to the point it exits the pyramid is also 70 cubits. This gives two side lengths of a square with an area of one-half acre. The diagonal length of the shaft is 99 cubits, the side length of one ancient Egyptian acre. The perimeter of the pyramid at ground level is 1760 cubits (440 × 4). The perimeter/height ratio is 1760/280 or 6.28 or 2π. The acreage of the vertical cross section of the pyramid is also 6.28 or 2π. The horizontal acreage of the pyramid at ground level is 19.75 or 2π². The horizontal acreage of the pyramid at the height of the floor of the king’s chamber is 9.87 or π². The side length of the pyramid at the height of the floor of the king’s chamber is equal to the 99 cubit side length of the ancient Egyptian acre times π. The side length of the pyramid at ground level is equal to the 140 cubit side length of two acres times π.
The slant height of the pyramid divided by one half of the base length (356/220 = 1.618) equals φ. In the 16th century Johannes Kepler studied the unique properties of a right triangle with the short side equal to one and the hypotenuse equal to φ. The long side of this triangle is equal to the square root of φ. Today this is known as the Kepler triangle:
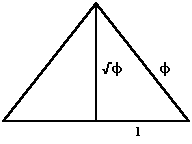
The hypotenuse (slant height) of the triangle times the short side (½ of the base length) is equal to φ (φ × 1 = φ). The long side (height) squared is the same (√φ² = φ). This is exactly how Herodotus correctly described the area of the sides of the pyramid (slant height × ½ base length) being the same as the area of the height squared. It is unlikely that the statement by Herodotus was based on his own calculations. He did not give any linear measures for the pyramid, it is unlikely that he could have measured or calculated the height of the pyramid so precisely and while the statement of 8 plethra for the sides and the height squared is true for ancient Egyptian acres with side lengths of 99 cubits, it is not true for the Greek units of measure used by Herodotus. It is more likely that Herodotus simply reported information he obtained from ancient Egyptian sources.
The area of the base of the pyramid is 193,600 (440 × 440) square cubits. The area of the base times φ is equal to the surface area of all four sides of the pyramid. A circle with a diameter of one cubit (seven palms) has a circumference of three cubits and one palm (22 palms). 22/7 equals 3.1428, a very close approximation to π that was used in the great pyramid. The slope (rise/run) of the pyramid is the height over the half base, or 280/220. This reduces to a slope of 14/11 or four cubits over three cubits and one palm or 4/π. If the height of the pyramid is taken as the radius of a sphere, the surface area of all four sides of the pyramid times π is equal to the surface area of the sphere and the volume of the pyramid times π times φ is equal to the volume of the sphere. Taking the height of the pyramid as the radius of a circle, the area of the circle is equal to the area of the base times 4/π and the area of the circle times 4/π is equal to the surface area of all four sides of the pyramid. The area of the base of the pyramid plus the area of the circle equals 440,000 square cubits. The circumference of the circle is equal to the perimeter of the pyramid:
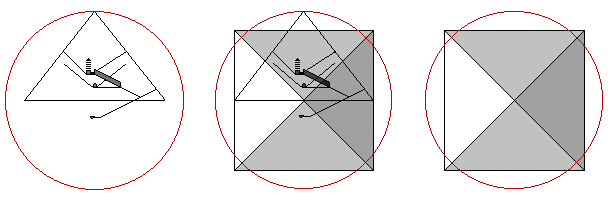
If the height of the pyramid is taken as the diameter of a sphere, the surface area of all four sides of the pyramid is equal to the surface area of the sphere times 4/π and the volume of the pyramid is equal to the volume of the sphere times π/2. Taking the height of the pyramid as the diameter of a circle, the circumference of the circle is equal to the base length of the pyramid times two and the area of the circle is equal to the area of the vertical cross section of the pyramid:
The diagonal of the base length of the pyramid at ground level is 622.25 cubits. The slope of the slant edges of the pyramid have run/rise ratio of 311.13/280 or 10/9 (one half of the base length diagonal over the height). The slope of the sides of the pyramid have a run/rise ratio of 11/14. The denominator in both cases is the height while the numerator of 10 is is the diagonal half base and the numerator of 11 is the half base. Multiplying 14 by 9 produces a common denominator of 126. Multiplying the diagonal half base of 10 by 14 gives 140 for the diagonal half base. Multiplying the half base of 11 by 9 gives 99 for the half base. The height of 126 cubits with a diagonal half base of 140 cubits and a half base of 99 cubits are the dimensions of the pyramid from the height the king's chamber shafts exit the pyramid.
The perimeter of a square with a diagonal length of 1.111 is also equal to π (1.111/1.414 × 4 = π). Since 1.111/1.000 is equal to 10/9, the circumference of a circle with a diameter of nine is equal to the perimeter of a square with a diagonal length of ten.
With a height for the pyramid of four, the diagonal half base is 4.444 (10/9 = 4.444/4), the half base is π and the slant height is π × φ. The diagonal half base divided by the square root of two gives the half base of π (4.444/1.414 = π). The square of the diagonal half base (4.444 × 4.444) is 19.75 or 2π², the same figure as the acreage of the base of the pyramid.
See Also:
Formulas for Areas and Volumes