Untitled Document

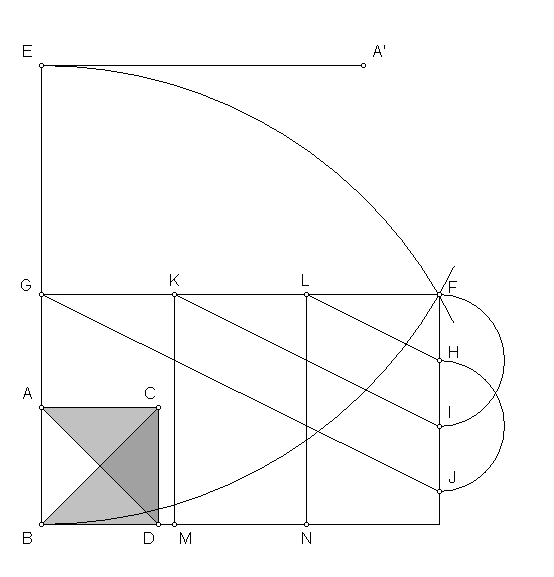
Construct a square (ABCD). Mark the midpoint of AB at E, mark the midpoint of AE at F and mark the midpoint of AF at G. Extend the diagonal AD to point H. Arc AG to point I. Extend a line from point I, perpendiculat to AH. Arc ID to point K. Arc KI to point L. Extend a line from point K, perpendicular to IL, to point M. Mark the midpoint of KL at N. Arc NM to point A'. IK is equal to ID and K-A' is equal to IK times phi. Thus I-A' is equal to ID times phi squared.

Given sidelengths for the great pyramid of 439.835 cubits (as indicated by surveys of WMF Petrie and JH Cole), The diagonal of the baselength is 622.020 cubits and 1/8th of the baselength (AG) is 54.9747 cubits, resulting in a length of 676.999 cubits for segment ID. 676.999 times phi squared (2.618.0339) equals 1772.4 cubits. This is the square root of pi times 1000. Segment ID + I-A' is 2449.4 cubits (1772.4 + 676.999). 2449.4 is the square root of six times 1000.

Since both segments ID and I-A' are at 45 degree angles, the vertical (NS) distance from segment BD (the northern edge of the great pyramid) to point A' is equal to 2449.4 cubits divided by the square root of two, or 1732 cubits. This is the square root of three times 1000. This is also the observed distance between the north edge of the great pyramid and the south edge of the third pyramid.. The horizontal (EW) distance from AB (the eastern edge of the great pyramid) to point A', is equal to 1772.4 cubits minus 54.9747 cubits (1717.4 cubits), divided by the square root of two equals 1214.4 cubits. Point A' marks the SE corner of the third pyramid.

Draw a horizontal line from A', intersecting a vertical line from AB at point E. Mark the intersection point F of arcs BE and EB. Draw a horizontal line from point F to EB at point G. Given the length of 1732 cubits for BE, the length of FG is 1500 cubits. Draw a vertical line from point F and mark point H on the line. Arc HF to point I and arc IH to point J. FH = HI = IJ. Draw segment JG. Construct segment IK parallel to segment JG. Construct segment HL parallel to segment JG. Points K and L trisect segment FG. GK = KL = LF = 500 cubits. Draw a horizontal line from BD. Draw a vertical line from point K to point M and draw a vertical line from point L to point N. BM = 500 cubits. BN = 1000 cubits.

Arc BN to point F. BN = BF = 1000 cubits. Mark the intersection point G of a horizontal line from point F and a vertical line from point N. Arc BG to point H. BH is equal to 1000 cubits times the square root of two, or 1414.2 cubits. Mark the intersection point C' of a horizontal line from point A' and a vertical line from point H. This is the southwest corner of the third pyramid. Arc C'-A' to point D'. This is the northwest corner of the third pyramid. Mark the intersection point B' of a horizontal line from D' and a vertical line from A'. B' is the northeast corner of the third pyramid.

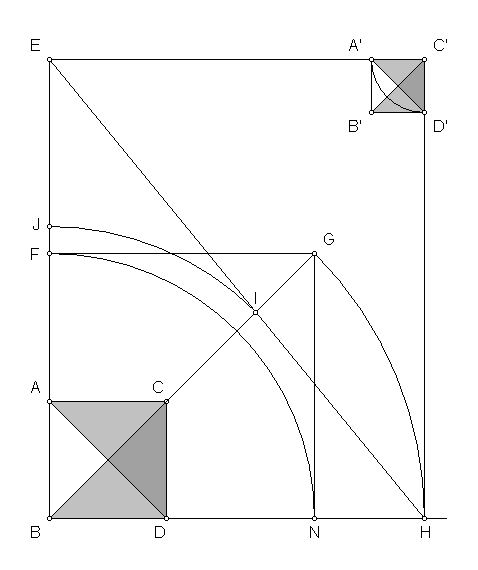
Draw segment EH and mark point I. Arc BI to point J. The length of BJ is 1101 cubits.

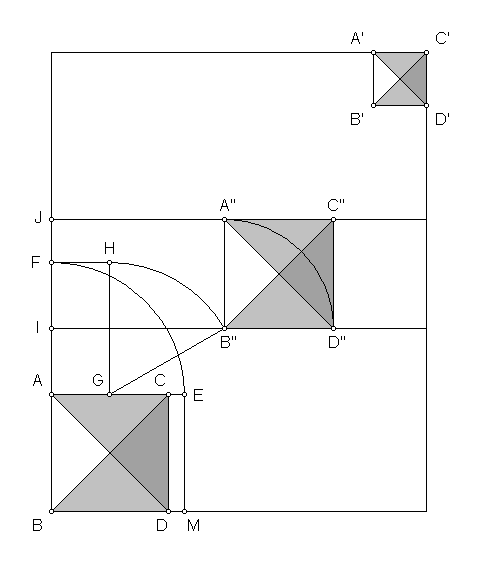
Mark the intersection point E of a horizontal line from point C and a vertical line from point M. Arc AE to point F. Mark the midpoint of AC at point G. Mark the intersection point H of a horizontal line from point F and a vertical line from point G. BM = AE = AF = GH = 500 cubits. Mark the midpoint of segment AF at point I. Draw a horitonal line from point I. Arc GH to point B". Mark the intersection point A" of a horizontal line from point J and a vertical line from point B". Arc B"-A" to point D". Draw a vertical line from D" and mark the intersection point C".

The length of segment G-B" is 500 cubits. G-B" is the hypotenuse of a right triangle. The short (vertical) side of the triangle is 250 cubits. The long (horizontal) side is 433 cubits. Since the long side begins at the EW midpoint of the first pyramid, the horizontal (EW) distance from the west side of the great pyramid to the east side of the second pyramid is 213 cubits (433 - 220 = 213) The northern edge of the second pyramid is 250 cubits south of the southern edge of the great pyramid (IA = 250 cubits). The sidelengths of the second pyramid are 411 cubits (BJ = 1101 cubits, minus AB (440 cubits), minus IA (250 cubits) = JI (411 cubits). This is in exact accordance with the surveyed size and location of the second pyramid in relation to the great pyramid.

The NS distance from the northern edge of the great pyramid to the southern edge of the third pyramid that is produced by the construction above is 1732 cubits, equal to the square root of three times 1000 cubits, in precise accord with the surveyed distance. This construction produces an EW distance from the eastern edge of the great pyramid to the western edge of the third pyramid of1414.2 cubits, equal to the square root of two times 1000 cubits.. This is three cubits shorter than the distance as surveyed by Petrie, although it has been previously suggested the outer EW measure was intended to equal the square root of two times 1000 cubits.. This construction produces a baselength of 200 cubits for the third pyramid. This is one and a half cubits shorter than the baselength for the third pyramid that was reported by Petrie, although several surveyors, including Petrie himself, have suggested that 200 cubits may have been the intended baselength of the third pyramid.