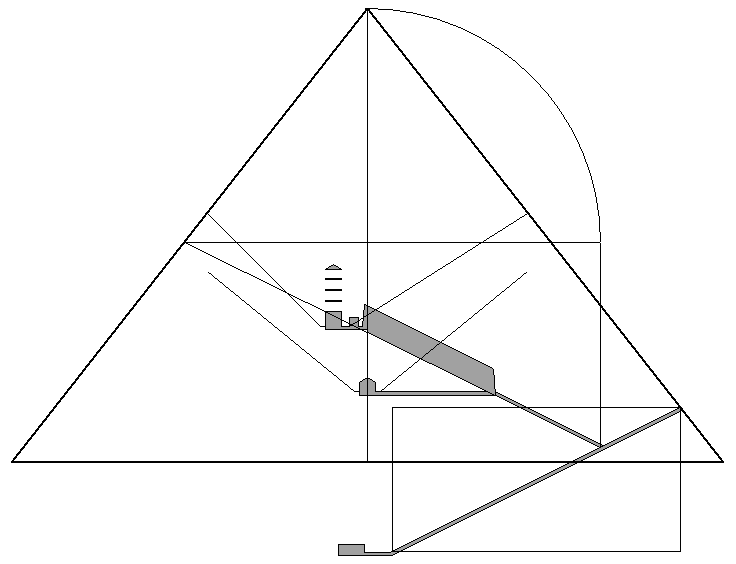
GREAT PYRAMID ENTRANCE PASSAGE
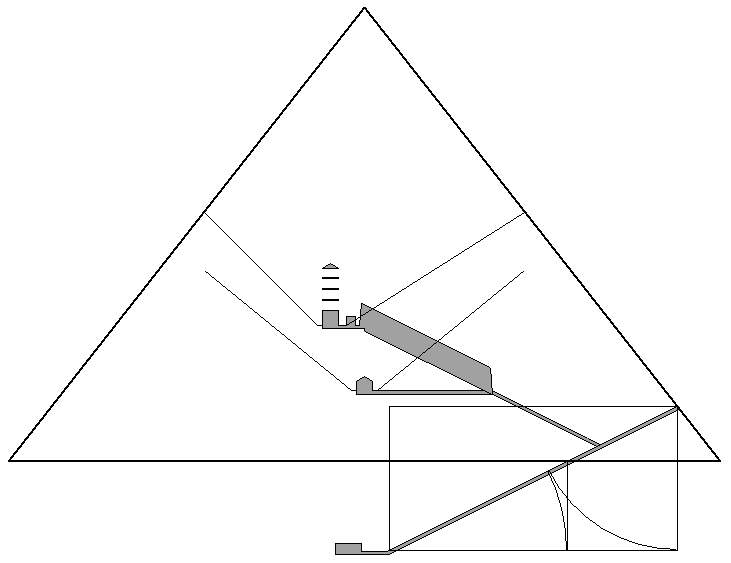
The entrance passage exits the great pyramid at the 19th course of masonry. The height of the passage along the sloping outer casing is equal to the height of the 19th course. The floor of the passage intersects the outer edge of the casing at the bottom of the 19th course and the roof of the passage intersects the outer edge of the casing at the top of the 19th course. Petrie directly measured the height of the top of the 19th course at 705.97 inches above ground level at the point where the entrance passage exits the pyramid. Petrie also directly measured the entire length of the sloping roof of the entrance passage at 4133 inches. The entrance passage has the same slope as the diagonal of a double square: Two units across for each one unit down. Based on the length and slope of the passage, Petrie calculated that the roof of the entrance passage terminates 1142.8 inches below ground level. Petrie believed that the margin of error in his calculated figure for the depth of the end of the roof of the passage below ground level was within one inch. Ground level divides the entrance passge into a golden section, within a margin of error of one-half of one inch, over the 4133 inch length of the roof of the passage:
705.97 x phi (1.618034) = 1142.3
The sides and the diagonal of a double square are divided into golden sections (1.618:1) as follows: Segment BD is arced to the diagonal at point E. Segment CE is arced to point F. A vertical line from point F divides the diagonal and the sides of the double square into golden sections at point G.
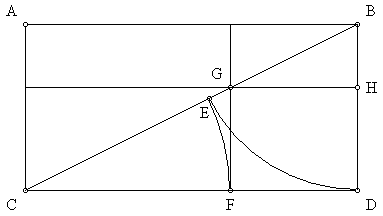
The Fibonacci series of numbers begins with 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... Given a length of 89 cubits for segment BD, segment CD is 178 cubits and segment CB is 199. Segment DH is 55. Segment BH is 34. Segment CF is 110. Segment DF is 68. Segment CG is 123. Segment BG is 76.
In the Great Pyramid, the height of the beginning of the roof of the entrance passage is 34.2 cubits above ground level. The depth of the end of the roof is 55.4 cubits below ground level. The total length of the roof is 200.4 cubits. The sloping roof of the entrance passage continues approximately 22 inches beyond the end of the floor of the passage. The axis of the entrance passage begins 34 cubits above ground level, at the outer edge of the casing of the pyramid, and ends directly above the end of the sloping floor of the passage. The axis of the entrance passage is is 199 cubits long and ends 55 cubits below ground level.
The diagonal of the double square is divided into the ratio of phi squared to one (2.618:1) as follows: Arc segment HD to point I. A vertical line from point I intersects AB at point J. BJ is arced to point K on the diagonal line. Point K divides the diagonal line into the phi square ratio of 2.618:1.
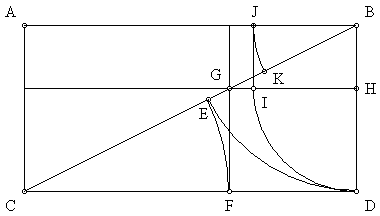
Given a length of 89 cubits for segment BD, segment BK is 55 cubits and segment CK is 144 cubits. 144:55 = 2.618:1. Segment GK is 21 cubits. The 55:21 ratio also equals 2.618:1. All of the lengths in these two phi square ratios are found in the sequence of Fibonacci numbers. Just as the adjoining numbers of the Fibonacci sequence express the phi ratio of 1.618:1, each two numbers, skipping a number, express the phi square ratio.
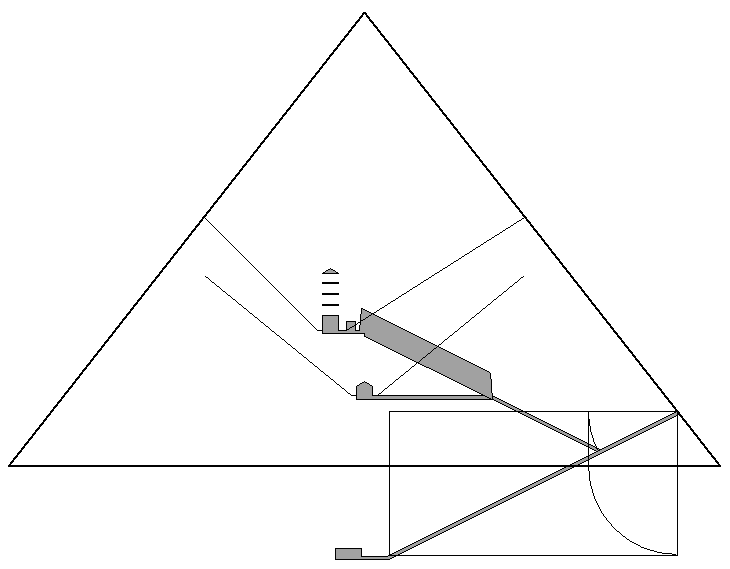
The roof of the entrance passage intersects the outer casing of the pyramid 34.2 cubits above ground level. The roof of the entrance passage intersects the floor of the ascending passage 55.1 cubits from the intersection point of the roof of the entrance passage and the outer casing of the pyramid. The axis of the entrance passage intersects the outer casing of the pyramid 34 cubits above ground level. This point is .2 cubits north of the intersection point of the roof of the passage with the outer casing of the pyramid. The floor of the ascending passage intersects the axis of the entrance passage .3 cubits north of the intersection point of the roof of the entrance passage and the floor of the ascending passage. 55.1 plus .2 minus .3 equals 55 cubits. The floor of the ascending passage divides the entire 199 cubit length of the axis of the entrance passage into the ratio of phi squared to one, within a surveyed margin of error of less than one inch. This point, shown in the upper diagram above as point K, is referred to below as the axis point.
The sloping length from the axis point to the end of the axis of the entrance passage is 144 cubits. The axis point is also 144 cubits north of the vertical midline of the pyramid. Arcing the 144 cubit length of axis of the entrance passage from the axis point marks the vertical midline of the pyramid, as shown below:

The axis of the entrance passage exits the outer casing of the pyramid 34 cubits above ground level. This height times four (34 x 4 = 136), plus the 144 cubit length from the axis point to the vertical midline of the pyramid, marks the 280 cubit height of the pyramid as shown below.
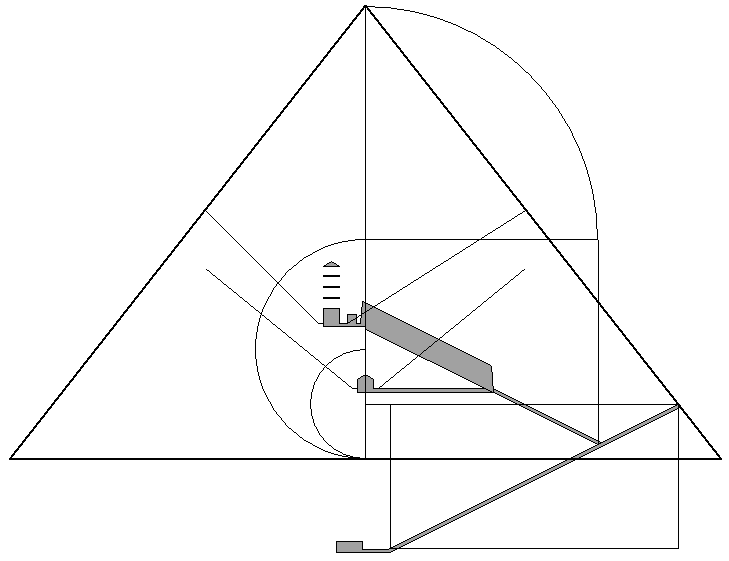
Given a double square with a side equal to 89 cubits, the precise golden section division of the side is 89/1.618034 = 55.005. 55.005/1.618034 = 33.995. The precise division of the diagonal is as follows: 89 x 2.236068 = 199.01. 199.01/3.618034 = 55.005. 199.01 - 55.005 = 144.005. Based on the geometric construction above, the height of the pyramid, up from the height the axis of the entrance passage exits the pyramid is 245.99 cubits (33.995 x 3 plus 144.005 = 245.99) The horizontal distance from the point the axis of the entrance passage exits the outer casing, to the vertical midline of the pyramid, is 193.203 cubits (55.005/1.118034 = 49.198. 144.005 plus 49.198 = 193.203). 245.99/193.203 = 1.27322. Four divided by 1.27322 equals 3.1416.
The height of the pyramid based on this geometric construction is 279.985 cubits (33.995 x 4, plus 144.005). A line from the top of the pyramid to the point the axis of the entrance passage exits the pyramid, extended to ground level, produces a base length for the pyramid at ground level of 439.8 cubits. This is in precise agreement with Petrie and Cole's survey data, and produces a pi ratio of 3.1416:1 for the height of the pyramid as the radius and the baselength of the pyramid as the circumference of a circle.
In the diagram below, the horizontal line 135.98 (33.995 x 4) cubits above ground level is extended to the southern edge of the pyramid. A line from this point to the axis point marks the floor of the ascending passage and the grand gallery. This line is within one inch of the surveyed position of the beginning of the floor of the ascending passage and within two inches of the surveyed position of the end of the floor of the grand gallery at the vertical midline of the pyramid. The angle of the floor of the ascending passage/grand gallery based on this geometric construction is 26° 12'. in precise accord with Petrie's survey. The distance from the axis point to the end of the grand gallery at the midline of the pyramid is 160.55 cubits. The distance from the midline to the point 135.98 cubits above ground level on the southern face of the pyramid is 126.1 cubits. The ratio between the length of the floor of the ascending passage/grand gallery from the axis point to the midline of the pyramid, and the length of the extension to the southern face of the pyramid, is 1.2732/1 (160.55/126.1 = 1.2732). This is precisely the same ratio as the height and the half base of the pyramid that is produced by these geometric constructions. The extension of the floor of the ascending passage/grand gallery is also within 1/10th of one cubit of the surveyed position of the south edge of the ceiling of the king's chamber.