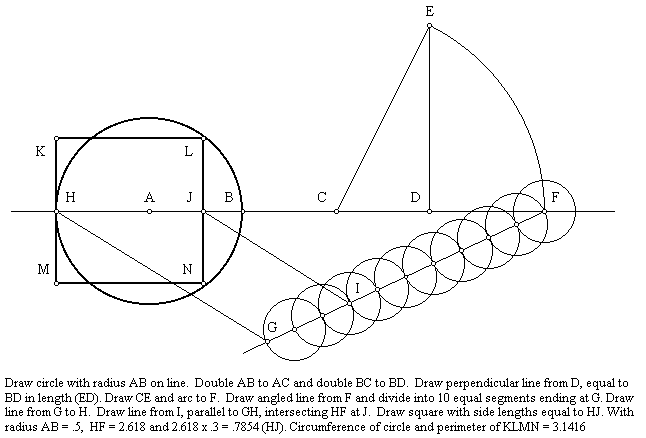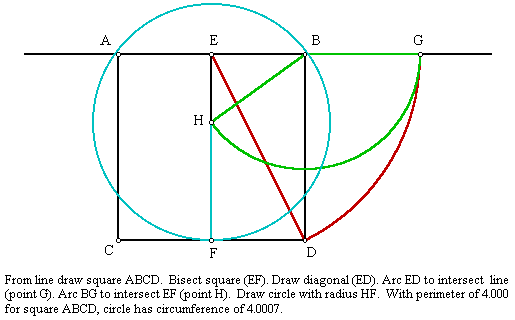
SQUARING THE CIRCLE
“Using only a straightedge and a compass, draw a circle that has the same circumference as the perimeter of a square.” This was a challenge issued by ancient Greek geometers. It has been suggested that the great pyramid solved this problem since the height of the pyramid taken as the radius of a circle gives a circumference equal to the perimeter of the square base of the pyramid. Over 100 years ago it was demonstrated mathematically that because pi is an irrational number, it is impossible to exactly square the circle with a straight edge and a compass, so perhaps a fairer challenge would be the simplest solution that gives a circumference that is most nearly equal to the perimeter of the square. Here is a simple solution that gives a circumference that is very close to the perimeter of the square:
Mathematical proof as follows:
Given a length of 1 for the sides of the square, the length of ED is 1.118034 (EFD is a right triangle. EF is 1 and FD is .5. The square of these two sides added together equals the square of the hypotenuse. EF squared is 1 and FD squared is .25. 1 plus .25 is 1.25 and the square root of 1.25 is 1.118034). EG is equal to ED. EB is .5 so EG minus EB gives .618034 for BG. HB is equal to BG (.618034). HEB is a right triangle with the right angle at E. The hypotenuse of the triangle is HB (.618034). EB is .5. The square of hypotenuse minus the square of one side equals the square of the other side. The square of HB (.381966), minus the square of EB (.25) equals .131966 for the square of side EH. The square root of .131966 is .36327 for the length of EH. One minus EH (.36327) gives HF (.63673). A circle with a radius of .63673 has a circumference of 4.00069 (.63673 x 2 gives a diameter of 1.27346 and 3.14159 x 1.27346 = 4.00069).
Here is another geometric solution using a straightedge and a compass that is based on φ²/5 = π/6. The figure is more complicated but the perimeter of the square and the circumference of the circle are more nearly equal.