BENT PYRAMID GEOMETRY
The northern (Red) pyramid at Dashur has a base length of 420 cubits and a height of 200 cubits. The sides of the right angle formed by the half base and the height are 210 and 200 cubits. The slant height (hypotenuse) of the pyramid is 290 cubits. This is a 10x expression of the Pythagorean 20-21-29 right triangle (20² + 21² = 29²). The upper part of the southern Bent pyramid at Dashur has the same or very nearly the same angular dimensions as the northern Red pyramid. The ratio between the slant height and the half base of 29/21 = 1.380952 is very nearly the same as the ratio of φ² + 1 / φ² = 1.381966. In The Temple of Man, Schwaller de Lubicz suggests that the intended ratio between the slant height and the half base of the upper part of the Bent is the phi proportion of φ² + 1 / φ² and that the ratio between the height and the half base of the lower part of the Bent is also φ² + 1 / φ². This ratio may be geometrically constructed as follows:
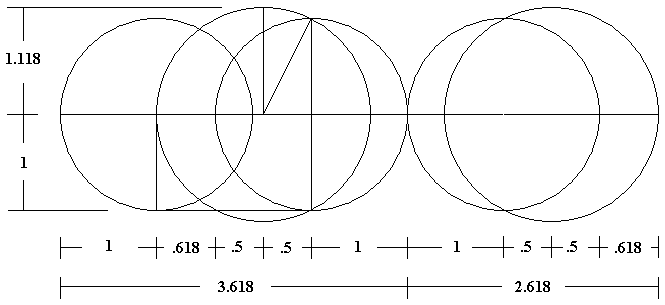
The smaller circles have a radius of one. The diagonal line from the midpoint of the radius to the top of the smaller circle forms the larger circle with a radius of 1.118. The radius of the smaller circle (1), plus one half of the radius of the smaller circle (.5), plus the radius of the larger circle (1.118), equals phi squared (2.618). An additional circle with a radius of one is centered on the left side of the larger circle to give the length of phi squared plus one (3.618).

The 3.618 segment is arced to the vertical line, producing right triangles with a height of phi squared plus one over a half base of phi squared.
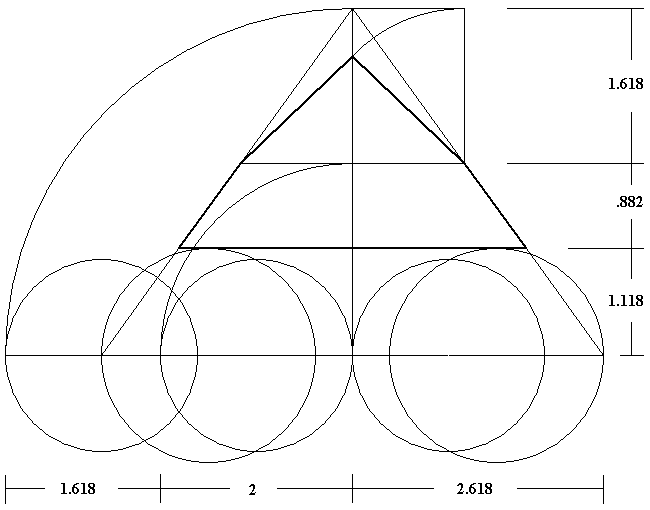
The radius of the larger circles is 1.118. The top of the vertical radius of the larger circles marks ground level for the pyramid. The diameter of the smaller circles is 2. The diameter of the smaller circle is arced to the midline of the pyramid, marking the height of the bend. This point is .882 above ground level and 1.618 below the apex of the triangle formed by the angle of the lower part of the pyramid. The ratio between the slant height and the half base of the upper part is equal to the ratio between the height and the half base of the lower part. Thus, the 1.618 height is arced to the midline of the pyramid to give a slant height of 1.618 for the upper part of the pyramid.

Given a scale of one unit equals 100 cubits, the height from ground level to the apex of the triangle formed by the angle of the lower part of the pyramid is 250 cubits (361.8 - 111.8). The half base of the pyramid at ground level is 180.9 cubits (250 x 2.618/3.618 = 180.9). The full base length of the pyramid is 361.8 cubits, a direct expression of phi squared plus one, equal to the height of the original triangle in the constructions above. This base length is in precise accord with W. M. F. Petrie's survey. Given a cubit of 20.62 inches, his measure of the west side of the pyramid was 361.79 cubits, an error of only one-hundredth of one cubit. The intended height of the pyramid is generally considered to be 200 cubits. This construction gives a height of 199.9 cubits (88.2 + 111.7). This construction explains the relationship between the lower part and the upper part of the pyramid: The proportional height of the lower part is equal to the proportional slant height of the upper part. This construction also explains the height of the bend, producing a slant height of phi times 100 for the upper part of the pyramid and a height of phi times 100 for the extension of the lower part of the pyramid.