
PROPOSED DESIGN SPECIFICATIONS FOR THE GREAT
PYRAMID AND FOR THE SITEPLAN OF THE GIZA PLATEAU
JIM ALISON
In the 1880's W. M. Flinders Petrie carefully surveyed the interiors and the exteriors of the pyramids at Giza. [1] Based on all of Petrie's findings, he concluded that the basic unit of measure used by the builders of the pyramids was 20.62 inches long. This unit of measurement is known as the royal cubit. While all of the proportions and ratios demonstrated by the structures at Giza are the same regardless of the unit of measure, application of the royal cubit makes many of the special geometric and mathematical relationships at Giza more readily apparent. These relationships are also more readily apparent when they are reduced to simple fractions.

The side lengths of the Great Pyramid at ground level are 440 cubits. The side length times the square root of two (1.4142) gives a horizontal diagonal at ground level of 622.25 cubits. Although the capstone of the Great Pyramid has been missing since antiquity, the theoretical height of the completed pyramid, calculated from the side length and the slope of the faces, is 280 cubits. The floor of the king's chamber is 82 cubits above ground level. The height of the pyramid up from the floor of the king's chamber is 198 cubits. The 280 cubit height divided by the square root of two is 198 cubits. The side lengths of the pyramid at the height of the floor of the king's chamber are 311.13 cubits, equal to one-half of the horizontal diagonal of the pyramid at ground level. The horizontal diagonal of the pyramid at the height of the floor of the king's chamber is 440 cubits, equal to the side length of the pyramid at ground level. The horizontal area of the pyramid at the height of the king's chamber is one-half of the area at ground level:
440² = 193,600 cubits
311.13² = 96,800 cubits
96,800 x 2 = 193,600
The formula for the area of the vertical cross section of the pyramid is 1/2 baselength x height. The area of the vertical cross section of the pyramid from the height of the king's chamber is also one half of the area of the vertical cross section of the pyramid:
220 x 280 = 61,600
155.56 x 198 = 30,800
30,800 x 2 = 61,600
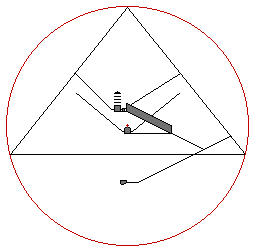
The king's chamber shafts exit the pyramid 154 cubits above ground level. The height of the pyramid up from the point where the shafts exit the pyramid is 126 cubits. The side length of the pyramid at this height is 198 cubits. The horizontal diagonal at this height is 280 cubits, the same as the overall height of the pyramid. The height of the entire king's chamber and shafts complex, from the floor of the chamber to the point where the shafts exit the pyramid, is 72 cubits.
The diagonal shafts extending from the king's chamber and the queen's chamber are 8-9 inches high and 8-9 inches wide. In 1993 Rudolph Gantenbrink sent in a miniature robot to measure the distances and angles of these shafts. [2] The shafts from the queen's chamber stop underneath the point where the shafts from the king's chamber exit the pyramid. Small doors are located at the end of the queen's chamber shafts and in 2002 another small robot drilled a hole through the door at the end of the southern shaft, revealing a small empty chamber.
Gantenbrink's robotic survey of the shafts in the Great Pyramid produced the following angular measurements:
| Upper southern shaft: 45° | Upper northern shaft: 32° 36' | |
| Lower southern shaft: 39° 36' | Lower northern shaft: 39° 7' |
Gantenbrink measured the angles of ascent of the upper (king's chamber) shafts all the way through, from inside and outside, and based on his survey data, he concluded that the intended slope of the upper southern shaft was 1/1 (45°) and that the intended slope of the upper northern shaft was 7/11 (32° 28' 16''). This slope for the upper northern shaft was within his narrowly defined margin of error for his survey data and it is exactly one half of the rise of the slope of the exterior faces of the pyramid (the height of 280 cubits over a half base of 220 cubits equals 14/11).
The King's chamber is 10 cubits wide. The north wall of the King's chamber is 16 cubits south of the vertical axis of the pyramid and the south wall of the chamber is 26 cubits south of the vertical axis of the pyramid. The shaft outlets are two cubits above the floor of the chamber, or 84 cubits above ground level. The northern shaft runs horizontally for five cubits before beginning it's ascent. The southern shaft runs horizontally for three cubits before beginning it's ascent. Extended downward, the intersection point of the shafts is five cubits below the floor of the chamber, or 77 cubits above ground level. This height is also 77 cubits below the height the shafts exit the pyramid. The intersection point is 22 cubits south of the vertical axis of the pyramid. 22 cubits south of the vertical axis of the pyramid is 77 cubits north of the point the southern shaft exits the pyramid and 121 cubits south of the point the northern shaft exits the pyramid. This gives sides of 77/121 (7/11) for the northern shaft as extended and 77/77 (1/1) for the southern shaft as extended.
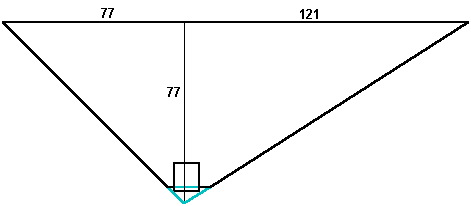
The vertical rise of the extended part of the shafts is 7 cubits and the horizontal run of the northern shaft is 11 cubits, while the horizontal run of the southern shaft is 7 cubits, demonstrating the rise and run of both shafts in the lowest possible whole numbers of cubits.
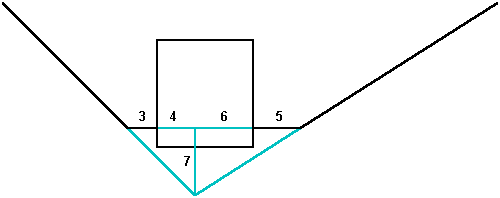
In 1995, John Legon pointed out that by extending the upper northern shaft beyond the face of the pyramid, it reaches the height of the apex of the pyramid 198 cubits north of it's exit point. This is a simple application of the 7/11 slope of the shaft: 126/198 = 7/11. Extended downward, the upper northern shaft intersects ground level 77 cubits north of the southern edge of the pyramid. The upper northern shaft intersects the southern face of the pyramid (as extended downward), 77 cubits south of the southern edge of the pyramid, 98 cubits below ground level. These points define a rectangle with a height equal to the height of the pyramid plus 98 cubits (below) and a width equal to the baselength of the pyramid plus 77 cubits on either side:

The diagonal of this rectangle is the upper northern shaft (as extended in both directions). The height of the rectangle is 378 cubits and the width is 594 cubits. The diagonal of the rectangle is 704 cubits: 378² + 594² = 704². Gantenbrink noted that many of the measures of the Great pyramid are multiples of 11. This width (54 x 11 = 594) and diagonal (64 x 11 = 704) are also multiples of 11.
Extended upward, the upper southern shaft intersects the height of the apex of the pyramid 126 cubits south of it's exit point: 126/126 = 1/1. This point is 72 cubits north of the southern edge of the rectangle. Extended downward, the upper southern shaft intersects ground level 55 cubits north of the midline of the pyramid. The upper southern shaft intersects the lower border of the rectangle 144 cubits south of it's northern edge. This point is also 54 cubits north of the exit point of the upper northern shaft. As extended downward, the upper shafts intersect below the king's chamber, 22 cubits south of the midline of the pyramid, 77 cubits above ground level and 77 cubits below the exit points of the upper shafts.
Unlike the upper shafts, the lower (queen's chamber) shafts do not exit the pyramid. Gantenbrink based his calculations of the angles of the lower shafts on measurements of less than one-half of the lower portion of the lower southern shaft and less than one-third of the lower portion of the lower northern shaft. Although there was a slight variance in Gantenbrink's survey data for the angles of the two lower shafts, Gantenbrink believes that the same slope may have been intended for these two shafts, making them symmetrical, since the queen's chamber is centered inside the pyramid. The shaft outlets in the queen's chamber are 44 cubits above ground level. The queen's chamber is 10 cubits wide and the shafts are horizontal for 3.7 cubits before beginning their angles of ascent. A slope of 9/11 equates to an angle of 39° 17' 22", in between Gantenbrink's survey data for the two lower shafts. With a slope of 9/11, the lower northern shaft, as extended upward beyond the pyramid, intersects the upper northern shaft at the height of the apex of the pyramid, 198 cubits north of the point the upper northern shaft exits the pyramid. [3]

The 198 cubit square, centered just above the queen's chamber in the diagram above, has the same dimensions as the side lengths of the pyramid at the height of the exit points of the upper shafts. The upper southern shaft extended downward forms a diagonal from the upper southern corner to the lower northern corner of the square. The length of this diagonal is 280 cubits, equal to the height of the pyramid (198 x 1.4142 = 280). The lower southern shaft extended downward intersects the upper southern shaft at the lower northern corner of the square. [4] The lower northern shaft extended downward intersects the lower southern corner of the square. As extended downward 98 cubits below ground level, the lower northern shaft intersects the lower border of the outside rectangle 55 cubits north of the southern edge of the pyramid. The distance of the lower northern shaft extended in both directions is 378 cubits up and 462 cubits across, a slope of 9/11.
Both of the lower shafts intersect the sides of the square 36 cubits below the upper shaft exit points and both of the lower shafts as extended upward cross over the height of the upper shaft exit points 44 cubits across from the exit points, also showing a slope of 9/11 (36/44). The upper northern shaft as extended downward also crosses ground level 44 cubits south of the exit point of the upper southern shaft. 56 cubits below the height of the upper shaft exit points, the faces of the pyramid are also 44 cubits across from the points where the upper shafts exit the pyramid, expressing the slope of the exterior faces: 14/11 = 56/44 = 280/220.
The point on the midline of the pyramid at groundlevel is the origin point of the arc in the diagram. The height of the upper shaft exit points is 154 cubits above ground level. The points where the lower shafts cross directly under the upper shaft exit points, are also 154 cubits from the midline of the pyramid at ground level. The distance of these diagonals may be calculated as the hypoteneuse of the right triangle formed by the height above ground level where the lower shafts cross under the upper shaft exit points (118 cubits) and the distance across from this point to the centerline of the pyramid (99 cubits): 118² + 99² = 154².
The two lower shafts intersect at the midline of the pyramid, 37 cubits above ground level and 81 cubits above the lower border of the square. This point is also 81 cubits below the point where the lower shafts intersect the sides of the square. The sides of the square are 99 cubits across from the intersection point of the lower shafts, demonstrating the same ratio as the slope of the lower shafts (81/99 = 9/11). All of the measures in the diagram above are integers and they are all multiples of 7, 9 and/or 11, supporting the proposed design specifications of 7/11, 9/11 and 11/11 for the diagonal shafts.
Michael Saunders recently proposed that in addition to the slope of the Great Pyramid, there is also a trigonometric relationship between the slopes of the shafts and π. The vertical axis of the pyramid is 280 cubits and the horizontal axis is 220 cubits (half-base). This proportion reduces to 14/11. Given a value of 22/7 for π , 14/11 is equal to 4/π. Since the tangent identity is the proportion between the vertical and the horizontal axis of a right triangle, the inverse tangent of 4/π is equal to the angle of the pyramid.

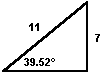
The 7/11 slope of the upper northern shaft is equal to 2/π . The inverse tangent of 2/π is equal to the angle of this shaft.
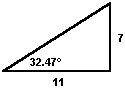
The sine identity is the proportion between the vertical axis and the hypotenuse of a right triangle. The observed angles of the lower shafts approximate the inverse sine of 2/π, making the proportion between the vertical axis and the hypotenuse of the lower shafts the same as the proportion between the vertical and the horizontal axis of the upper northern shaft. A vertical axis of 7 and a hypotenuse of 11 gives a horizontal axis equal to the square root of 72.
The results of Petrie's survey by triangulation, in inches, are as follows:
| NS Distance: | EW Distance: | Total Distance (angle west of due south): | |
| Centre of First to centre of Second Pyramid | 13931.6 | 13165.8 | 19168.4 at 43º 22' 52" |
| Centre of First to centre of Third Pyramid | 29102.0 | 22616.0 | 36857.7 at 37º 51' 6" |
| Centre of Second to centre of Third Pyramid | 15170.4 | 9450.2 | 17873.2 at 34º 10' 11" |
These measurements convert to cubits as follows:
| NS Distance: | EW Distance: | Total Distance | |
|
Centre of First to centre of Second Pyramid |
675.6 | 638.5 | 929.6 |
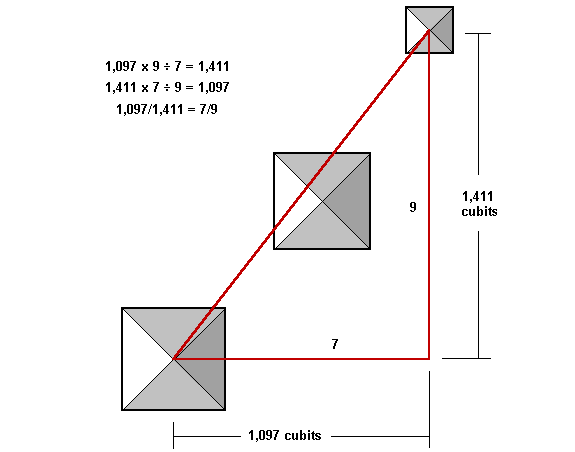
| Centre of First to centre of Third Pyramid | 1411.3 | 1096.8 | 1787.5 |
| Centre of Second to centre of Third Pyramid | 735.7 | 458.3 | 866.8 |
Petrie's measurements of the base lengths of the three main pyramids at Giza are as follows:
| Inches | Cubits | |
| First Pyramid | 9,068.8 | 440 |
| Second Pyramid | 8,474.9 | 411 |
| Third Pyramid | 4,153.6 | 201.5 |
The distance from the apex of the first pyramid to the apex of the third pyramid is 36,857.7 inches. This is the hypotenuse of the right triangle formed by the NS distance and the EW distance from apex to apex. The slope of this diagonal west of due south may be expressed as the fraction: 22,616/29,102. This reduces to almost exactly 7/9. The angle of the apexes of the first and third pyramids west of due south is 37° 51' 6". A true7/9 right triangle has an angle of 37° 52' 30''. The margin of error is just over one arc minute, or approximately 20 inches over a distance of 36,857.7 inches:
22,616 inches x 9 ÷ 7 = 29,078 inches
29,102 inches x 7 ÷ 9 = 22,634 inches
In cubits, the margin of error is within one cubit, over a distance of 1,787 cubits:
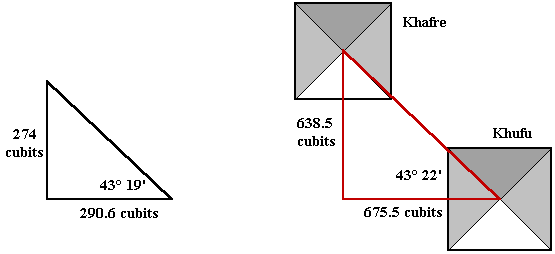
The distance from the apex of the first pyramid to the apex of the second pyramid is 19,168.4 inches. The slope of this diagonal west of due south may be expressed as the fraction: 13,165.8/13,931.6. This reduces to almost exactly 17/18. The angle of the apexes of the first and second pyramids is 43º 22' 52''. A true 17/18 right triangle has an angle of 43º 21' 48". The margin of error is just over one arc minute, or approximately eight inches over a distance of 19,168.4 inches:
13,165.8 x 18 ÷ 17 = 13,940.2
13,931.6 x 17 ÷ 18 = 13,157.6
The height of the second pyramid (Khafre's pyramid) is 274 cubits. The baselength of Khafre's pyramid is 411 cubits. The diagonal of the baselength of Khafre's pyramid is 581.2 cubits (411 x 1.4142). One half of the diagonal of the base is 290.6 cubits. As a result, the slope of the slant edge of the pyramid is 274/290.6, which reduces to 17/18 within a margin of error of less than one half of one cubit. The angle of the slant edge of Khafre's pyramid is 43° 19', within three arc minutes of a true17/18 right triangle and within four arc minutes of the angle of the diagonal from the apex of Khafre's pyramid to the apex of the first pyramid (Khufu).
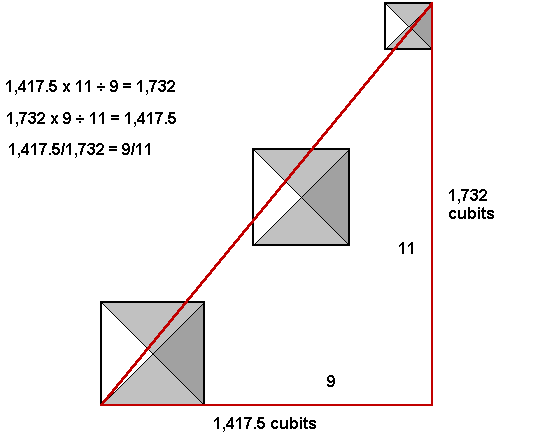
1096.8 + 220 + 100.75 = 1,417.5 cubits EW.
1411.3 + 220 + 100.75 = 1,732 cubits NS.
The slope of the diagonal from the NE corner of the first pyramid to the SW corner of the third pyramid is 1.417.5/1,732, which reduces to a slope of 9/11. The angle west of due south from the NE corner of the first pyramid to the SW corner of the second pyramid is 39° 17' 51". A true 9/11 right triangle has an angle of 39° 17' 22". The margin of error is less than 30 arc seconds:
Based on Petrie's measurements, John Legon diagrammed the relative positions of the three main pyramids at Giza as follows:
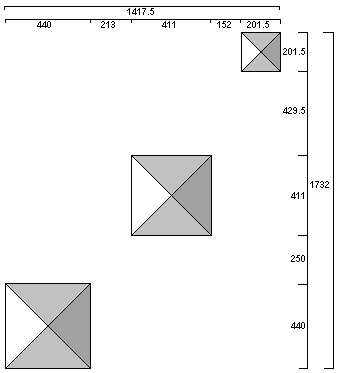
The NS distance between the southern edge of the first pyramid and the northern edge of the second pyramid is 250 cubits. Legon observed that in addition to the 250 cubit NS spacing between the first two pyramids, other measures are also based on 250 cubits multiplied by elementary square roots.
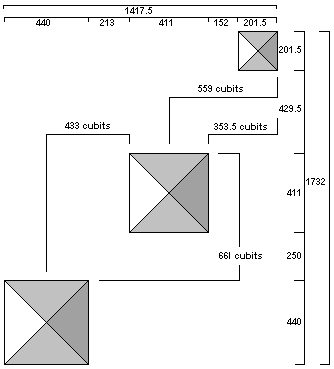
The square root of two is 1.414. The EW distance from the western edge of the second pyramid to the western edge of the third pyramid is 353.5 cubits:
250 x 1.414 = 353.5
The square root of three is 1.732. The EW distance from the center of the first pyramid to the eastern edge of the second pyramid is 433 cubits:
250 x 1.732 = 433
The square root of five is 2.236. The EW distance from the center of the second pyramid to the western edge of the third pyramid is 559 cubits:
250 x 2.236 = 559
The square root of seven is 2.646. The NS distance from the southern edge of the first pyramid to the southern edge of the second pyramid is 661 cubits:
250 x 2.646 = 661
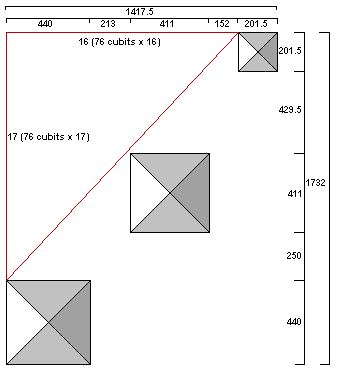
The third pyramid is 125.5 cubits high. The combined height of the pyramids is 280 + 274 + 125.5 = 679.5 cubits. This is equal to the two NS spaces between the three pyramids (250 + 429.5 = 679.5).
The sum of the two EW spaces (213 + 152) is 365 cubits, equal to the number of days in a year. [5]
Further evidence of the use of this unit of measure may be found in the distance from the western edge of the second pyramid to the eastern edge of the third pyramid (152 cubits [76 x 2 = 152]).
Each of the three main pyramids at Giza had a temple adjoining it and at the end of a causeway each of the pyramids had another temple, commonly referred to as the valley temples. The temple directly in front of the sphinx and right next to the second pyramid's valley temple is known as the sphinx temple.

The EW distance from the western edge of the third pyramid to the eastern edge of the second pyramid's valley temple and the sphinx temple is 2,000 cubits. The distance from the northern edge of the first pyramid to the southern edge of the third pyramid is 1,732 cubits. 1,732 is equal to the square root of three times 1,000. 2,000 is equal to the square root of four times 1,000. The diagonal of this rectangle is 2,645.75 cubits long. 2,645.75 is equal to the square root of seven times 1,000. This is a precise expression of Pythagoras theory in the form of:
√3² + √4² = √7²
The NS distance from the southern edge of Menkaure to the northern edge of Khufu's valley temple is 2,100 cubits. The EW distance from the western edge of Menkaure to the eastern edge of Khufu's valley temple is 2,800 cubits.
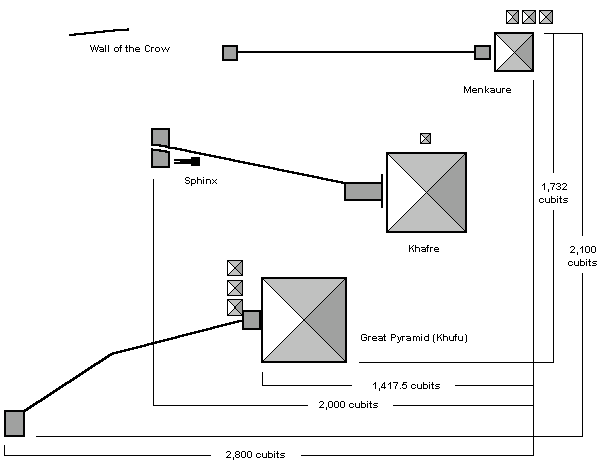
The diagonal of the rectangle described by the SW corner of Menkaure and the NE corner of Khufu's valley temple is 3,500 cubits long, demonstrating a 3-4-5 right triangle of 2,100 - 2,800 - 3,500 cubits.
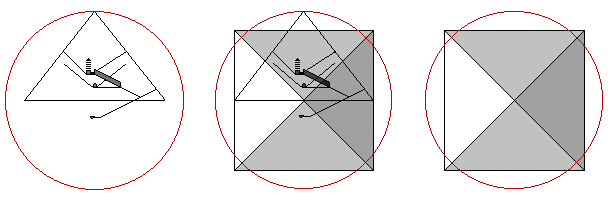
The Great Pyramid is 280 cubits high and the perimeter of the pyramid is 1760 cubits (440 x 4).
A circle with a radius of 280 cubits has a circumference (280 x 2 x 3.1428) of 1760 cubits.
The area of the base of the pyramid is 193,600 square cubits (440 x 440).
The area of the vertical section of the pyramid is 61,600 square cubits (280 x 220)
The area of the vertical section times π equals the area of the base:
61,600 x 3.1428 = 193,600.
The area of a circle with a radius of 280 cubits is 246,400 square cubits (π x 280²).
The area of the base of the pyramid plus the area of the circle is 440,000 square cubits. [5]
π (pi) is the ratio between the circumference and the diameter of a circle. The modern value for this ratio is 3.14159 to one. Because the radius of a circle is one-half of it's diameter, the radius times 2π also equals the circumference of the circle. The fraction 22/7 is an approximation for π that is known to have been used in ancient times: 22/7 = 3.1428. An equally accurate measure of the 2π relationship between the radius and the circumference of a circle is 44/7.
The 2π relationship between the height and the perimeter of the Great pyramid may be simply demonstrated based on the measures of the pyramid in cubits. Given the base lengths of 440 cubits, the perimeter of the pyramid is 1760 cubits (440 x 4). The height is 280 cubits. 1760/280 equals 44/7. The ancient ratio of 22/7 for the circumference of a circle also provides a simple solution to the age old problem of squaring the circle. Using this ratio, a circle with a diameter of 1.000 has a circumference of 3.1428. The perimeter of a square with a diagonal length of 1.111 is also equal to 3.1428 (1.111 ÷ 1.414 x 4 = 3.1428). Since 1.000/1.111 is equal to 9/10, this also means that the circumference of a circle with a diameter of nine is equal to the perimeter of a square with a diagonal length of ten, using the 22/7 ratio for the circumference of the circle.
Corner sockets cut into the bedrock below the Great Pyramid enabled Flinders Petrie to make precise measurements of the pyramid's original base lengths. These were his findings:
N: 9069.4 inches
E: 9067.7
S: 9069.5
W: 9068.6
Mean: 9068.8 inches
Although the base length of the pyramid is generally cited as 440 cubits, 9068.8 inches divided by 20.62 equals 439.8 cubits. Given that the error between the shortest side and the longest side is less than two inches, it is unlikely to have been an accident that all of the sides are about four inches short of exactly 440 cubits. With a ratio of 3.14142 to one, 439.8/280 expresses the modern value for π/2 much more accurately than 440/280 and it has been suggested that this is the reason the sides of the pyramid are just under 440 cubits. 439.82/280, an exact expression of our modern value for π/2, is less than one-half of one inch longer than the Great Pyramid's observed mean base lengths of 9068.8 inches.
With base lengths of 440 cubits, the diagonal length of the base of the pyramid is 622.25 cubits, but with base lengths of 439.82, the diagonal length is precisely 622 cubits. Given the side lengths of 311 cubits at the height of the floor of the King's chamber, the diagonal of the base at that height is also precisely 439.82 cubits.
2,238 ÷ 8 = 279.75
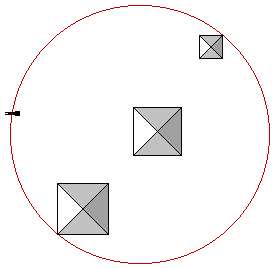
Since the height of the Great Pyramid times 2π is equal to the perimeter of the pyramid, the circumference of the circle that inscribes all three of the major pyramids at Giza is almost exactly four times the length of the perimeter of the Great Pyramid. This circle also neatly bisects the sphinx.
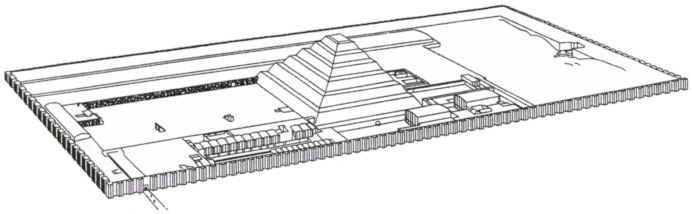
Jean-Philippe Lauer spent most of his life excavating the site of the step pyramid and he found that the pyramid was surrounded by a massive enclosure wall 34 feet high and 5,398 feet long. 34 feet is equal to 20 royal Egyptian cubits and 5,398 feet is equal to 3,141.5 cubits, a very precise expression of π times 1,000. Lauer's illustration below shows the original design of the pyramid complex, although the northern end of the complex is still only partially excavated and is shown filled with sand.
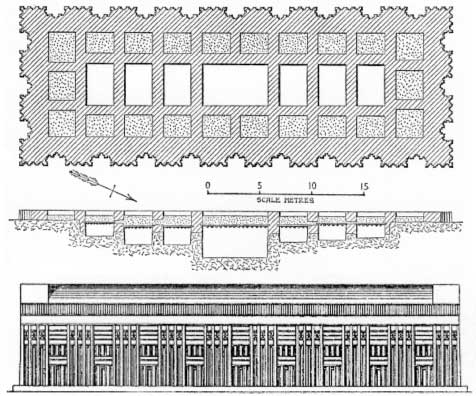
Djoser ruled during ancient Egypt's third dynasty, but Saqqara was a royal burial ground from the beginning of dynastic Egypt. In the 1950's, Walter Emery excavated several of the early dynastic tombs at Saqqara, including the tomb of Djer, the second pharaoh of the first dynasty following the unification of ancient Egypt. Emery's illustration of Djer's tomb below also suggests the ancient 22/7 ratio with a line of seven magazines surrounded by 22 supports.

220 ² + 53.5 ² = 226.5 ²
AB/BC = AC/AB = 1.618
Given a length of 1.618 for AB, BC is 1.000. AB plus BC = 2.618. φ² (1.618 x 1.618) also equals 2.618. φ² divided by five equals .5236. π (3.1416) divided by six also equals .5236, showing that π/6 = φ²/5
The φ ratio is the basis of the Fibonacci series of numbers and Fibonacci spirals. This is also the ratio between the length of the slant height (356 cubits) and the length of one half of the base (220 cubits) of the Great Pyramid:
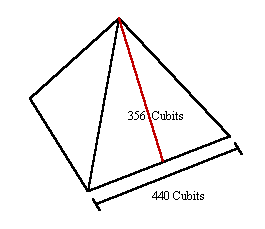
356/220 = 1.618
The surface area of the faces of the pyramid are 78,320 square cubits (356 x 220). The surface area of all four faces of the pyramid is 313,280 square cubits (78,320 x 4). The area of the base of the pyramid times φ is equal to the surface area of the faces of the pyramid (193,600 x 1.618 = 313,280).
Another important mathematical constant is 2.7182. Believed to have been discovered in modern times by Isaac Newton it is known as epsilon, the exponential number, and is designated by the small case Greek letter ε. This number is the base of the natural logarithms and is used to calculate continuous rates of growth and decay, among it's many mathematical applications. ε is illustrated by the process of compounding interest. $1.00 at 100% interest compounded annually yields two dollars at the end of the year. Compounding semi-annually yields $1.50 after six months and $2.25 at the end of the year. Compounding quarterly, the figure at the end of the year is $2.44. Increasing the frequency of compounding to infinity yields a year end figure equal to ε. In 2001 Rick Howard discovered that ε is also encoded in the Great Pyramid. [6] The pyramid's height of 280 cubits and half base of 220 cubits forms a right triangle with a lower angle of 51° 51' (51.85°) and an upper angle of 38° 9' (38.15°):
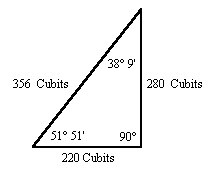
51.85 divided by 38.15 equals 1.3591. 1.3591 times two equals 2.7182. In other words, 51.85/38.15 = ε/2. Rick Howard also discovered that the base length of the pyramid in cubits is equal to ε times φ times 100: 2.7182 x 1.618 x 100 = 439.8. This confirms that both ε and φ were encoded in the size as well as the shape of the Great Pyramid.
1 : √φ : φ
This right triangle is known as the Kepler triangle because Johannes Kepler wrote about it in the 16th century, but this is the same right triangle that is found in the dimensions of the Great Pyramid:
220 : 280 : 356 = 1 : √φ : φ
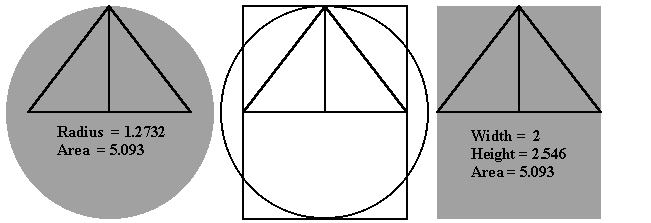
These ratios may be visualized by assigning a value of one to the half base of the Great Pyramid:

Since four divided by π is equal to √φ (accurate to 99.9%), the height, √φ, is also 4/π, as shown in the diagram. In The New View Over Atlantis, John Michell uses this diagram to show the ratios in the Great Pyramid. For a geometry course at Dartmouth College, Paul Calter also uses the value of one for the half base of the Great Pyramid in Squaring the Circle - Geometry in Art and Architecture. [7]
Given a half base of one, each baselength is two, so the perimeter of all four sides of the pyramid is eight. The circumference of a circle is equal to the radius times 2π. The circumference of a circle with a radius equal to the height of the pyramid (4/π) is 4/π times 2π. π cancels out, leaving 4 x 2 = 8, the same as the perimeter of the pyramid.
The formula for determining the area of a circle is:
π r²
The radius of 4/π (1.2732) squared is 1.621, so the area of the circle with a circumference equal to the perimeter of the pyramid is:
π (3.14159) x 1.621 = 5.093
The width of a rectangle times the height gives the area of the rectangle. The height of the pyramid is 4/π. Twice the height of the pyramid is 2.546:
1.2732 x 2 = 2.546
The baselength of the pyramid is two. A rectangle with one side equal to the baselength of the pyramid and the other side equal to twice the height of the pyramid, has the same area as a circle with a radius equal to the height of the pyramid.
With a height of √φ and a half base length of 1, the apothem is φ. The surface area of the faces of the pyramid is also φ (φ x 1 = φ). The surface area of all four faces of the pyramid is 4φ. The formula for calculating the surface area of a sphere is:
4 π r²
The radius (r) is √φ, the same as the height of the pyramid. The square root of φ squared is φ, so the surface area of the pyramid times π is equal to the surface area of a sphere with a radius equal to the height of the pyramid.
The formula for calculating the volume of a sphere is:
4/3 π r³
The radius (r) is √φ. √φ³ may also be expressed as φ times √φ (squaring √φ the first time gives φ, then times √φ again to get the cube), so the solution may be expressed as follows:
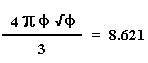
The formula for calculating the volume of a pyramid with a square base is:
1/3 base² x height
The base is two, so the base squared is four. The height is √φ, so the solution may be expressed as follows:

Comparing the solution for the volume of the sphere and the solution for the volume of the pyramid, the four above the line cancels out, the √φ above the line cancels out and the three below the line cancels out, leaving:
1.696 π φ = 8.621
The volume of the Great Pyramid times π times φ is equal to the volume of a sphere that has the same radius as the height of the pyramid and the same circumference as the perimeter of the pyramid.
In the examples above the half base of the pyramid is one and the full base length is two. If the full base length of the pyramid is one, the height is .6366 and so is the radius of a circle with a circumference of four, equal to the perimeter of the pyramid. A circle with a circumference of four has a diameter and an area of 1.2732. If the full base length of the pyramid is one-half, the height is .3183 and the perimeter is two. A circle with a circumference of two has a radius and an area of .3183.
In the examples above the dimensions of the pryamid are compared to a circle or a sphere with a radius equal to the height of the pyramid. The ratio between the height and the baselength of the pyramid also results in simple relationships betwen the pyramid and a circle or a sphere with a diameter equal to the height of the pyramid.
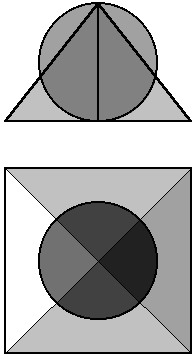
Given a baselength of two for the pyramid, the half base is one, the perimeter is eight and the area of the base is four. The height of the pyramid is1.2732. The area of the vertical cross section of the pyramid is 1.2732 and the volume of the pyramid is 1.698. The diameter of the circle/sphere is also 1.2732. The circumference of the circle is four, the area of the circle is 1.2732 and the volume of the sphere is 1.081.
The area of the vertical cross section of the pyramid is equal to the area of the circle.
The volume of the pyramid times two is equal to the volume of the sphere times π.
Given 1.272 (the square root of φ) for the height of the pyramid and the diameter of the circle, the slant height of the pyramid is 1.618 and the surface area of the pyramid is 6.472. The surface area of the sphere is 5.083. The surface area of the pyramid times π is equal to the surface area of the sphere times 4.
The king's chamber in the Great Pyramid is precisely 10 cubits wide and 20 cubits long. The ancient Egyptian royal cubit was divided into seven palms and palms were divided into four digits. All four of the walls of the king's chamber consist of five courses of equal height. Each of the courses is 64 digits, or16 palms high, so the total height of the chamber from the base of the walls to the ceiling is 320 digits or 80 palms or 11.428 cubits. Expressing all of the dimensions of the chamber in palms, the width is 70 palms, the height is 80 palms and the length is 140 palms, the proportions being 7 : 8 : 14, or 1 : 1 1/7 : 2. The length plus the height is 3 1/7, or 3.1428. In cubits, the length plus the height of the chamber (11.428 + 20) is 31.428 cubits. 31.428 cubits divided by the width of the chamber (10 cubits) equals 3.1428. The perimeters of the long walls of the chamber are 440 palms (80 x 2 plus 140 x 2), one seventh of the baselength of the pyramid. Dividing the perimeter of the wall (440 palms) by the length of the wall (140 palms), also demonstrates π: 440/140 = 22/7 = 3.1428.
The granite floor of the king's chamber is not connected to the walls and the top of the floor blocks are seven digits (one quarter of a cubit) above the base of the first course of the walls of the chamber. Thus, the height of the chamber from the top of the floor blocks to the ceiling is 11.18 cubits:
320 - 7 = 313 digits
313 digits ÷ 28 = 11.18 cubits
The square root of five is 2.236. The height of the chamber from the top of the floor blocks to the ceiling is equal to √5 x 5 cubits (2.236 x 5 = 11.18). The formula for calculating φ is √5 + 1 divided by 2:
2.236 + 1 = 3.236
3.236 ÷ 2 = 1.618
Given the height of the chamber from the top of the floor blocks to the ceiling of √5 x 5 cubits, the height plus one half of the width of the chamber (5), divided by the width of the chamber (10), equals φ ( 11.18 + 5 ÷ 10 = 1.618). 11.18 is also the square root of 125. The diagonal length of the floor of the chamber is 22.36 cubits, exactly twice the height. 22.36 is the square root of 500. This distance may be calculated as the square root of the squares of the length and the width of the chamber (400 + 100).
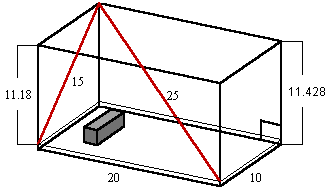
The diagonal length of the short walls of the king's chamber is 15 cubits. This may be calculated as the square root of the squares of the height and the width (125 + 100). The square root of 225 is 15. The diagonal length from upper corner to opposite lower corner is 25 cubits. This may be calculated as the square root of the squares of the length of the long side and the diagonal of the short side (400 + 225). The square root of 625 is 25. This is a 3-4-5 right triangle (15-20-25). The volume of the chamber is 2,236 cubic cubits. This may be calculated by multiplying the length times the width times the height (20 x 10 x 11.18). 2,236 is the square root of five times 1,000. 2,236 is also the square root of 5,000,000.
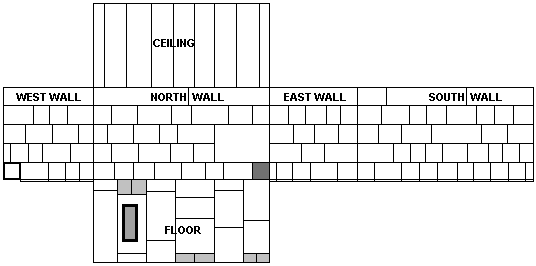
There are a total of 100 blocks in all four walls of the chamber. The dark square in the north wall is the entrance passageway into the chamber. The east wall has 18 blocks. The north wall has 27 blocks and the south wall has 36 blocks. The ceiling has nine beams. The floor originally had 18 blocks in six courses, although the floor presently has 21 blocks. The three blocks in the lightly shaded areas were pulled out by early explorers and have been replaced with six blocks. All of the joints between the blocks in the walls of the king's chamber are approximately 1/50th of an inch wide. In the 1970's and 80's J. P. Lepre conducted a 15 year study of the pyramids of Egypt, concentrating on the Great Pyramid. Lepre found that the southernmost block on the first course of the west wall was the one exception to the tightly fitted joints in the walls of the king's chamber. The joints around this block are 1/16th to 1/4 of an inch wide. Lepre also found that the base of this block is at the level of the floor blocks of the chamber, rather than a quarter of a cubit below the level of the floor, like all the other blocks on the first course of the walls of the chamber. Based on this information, Lepre proposed that this block may be blocking another passageway into or out of the king's chamber. To date, his requests for further investigations of this block have been denied by the Egyptian authorities. The west wall has 19 blocks, including the block that Lepre suggests is blocking a passageway. If Lepre is correct then the west wall would have 18 blocks with the passageway open and the number of blocks in all six surfaces of the king's chamber would be multiples of nine: Ceiling - 9; east wall, west wall and floor - 9 x 2; north wall - 9 x 3; and south wall - 9 x 4. This brings the total to 99 blocks in the walls, or 9 x 11.

These dimensions convert to 20.62 inch ancient Egyptian cubits as follows:
| Outside: | Inside: |
| Length: 4.346 | Length: 3.785 |
| Width: 1.867 | Width: 1.3 |
| Height: 2 | Height: 1.67 |
The outside volume of the coffer is 16.22 cubic cubits (4.346 x 1.867 x 2 = 16.22). The inside volume is 8.22 cubic cubits (3.785 x 1.3 x 1.67 = 8.22). This leaves a difference of eight cubic cubits that represents the solid bulk of the coffer. In other words, the bulk of the coffer equals a solid cube 2 cubits wide, 2 cubits long and 2 cubits high. Since the height of the coffer is 2 cubits, the bulk of the coffer is equal to a solid cube with sides the same length as the height of the coffer. The inside diagonal of the coffer is twice the height of the coffer (3.785² + 1.3² = 4²), just as the diagonal of the king's chamber is twice the height of the chamber.
The sum of the inside length and the inside width of the coffer is 5.085 cubits (3.785 + 1.3 = 5.085). φ x π is also equal to 5.085 (1.618 x 3.1428 = 5.085). The inside perimeter of the coffer (10.17 cubits) is twice the sum of the inside length and inside width. This equals 2φ x π. Since the height of the coffer is 2 cubits, the inside perimeter of the coffer is equal to the height of the coffer times φ times π. A circle with a radius of φ (1.618 cubits) has a circumference of 10.17 cubits (2φ x π = 10.17), equal to the inside perimeter of the coffer. This same circle has an area of 8.22 cubits (φ² x π = 8.22), equal to the inside volume of the coffer.
The coffer's outside volume of 16.22 cubic cubits is equal to the volume of a sphere with a diameter of π. [8] The formula for the volume of a sphere is:
4/3 π r³
π ÷ 2 = 1.5708 (radius)
1.5708³ = 3.875
3.875 x π = 12.17
12.17 x 4/3 = 16.22
16.22 is also the diameter of a sphere with a volume of 2,236 cubit cubits, equal to the volume of the king's chamber.
All of the passages in the great pyramid are two cubits (14 palms) wide. The transverse or perpendicular height of the ascending and descending passages is 16 palms, the same as the height of each of the courses of the king's chamber. The perimeters of the inclined passages are 60 palms (16 x 2 plus 14 x 2). Subtracting the height of 16 palms from the passage perimeter of 60 palms gives 44 palms or 6.2857 cubits. 22/7 x 2 = 6.2857.
The floor of the Grand Gallery is also two cubits wide although the base of the gallery is four cubits wide. Blocks one cubit high and one cubit wide run the entire length of the gallery on either side of the base. The walls of the gallery are comprised of seven overlapping courses. Each successive overlap is one palm narrower on each side, so the ceiling of the gallery is also two cubits wide. The width of the gallery at the third overlap is 22 palms or 3.1428 cubits. The half way point in the height of the gallery is towards the bottom of the third overlap and is marked by shallow grooves on both sides of the third overlap that run the entire length of the gallery. The diagram below is a crossection of the gallery.
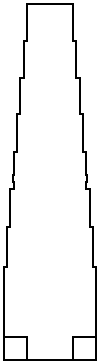
The antechamber is 7.236 cubits high and 5.64 cubits long. The upper width of the chamber is 22 palms or 3.14 cubits. Granite wainscots four palms wide line the lower portion of the east and west walls of the chamber, making the floor and lower portion of the chamber two cubits wide. Three vertical slots one cubit wide are carved from the top of the wainscots to the floor. These slots held stones blocking entrance to the king's chamber. A fourth slot that was not carved all the way down to the floor presently holds a block in place at the height of the ceiling of the passageway. Large semicircular hollows were carved into the top of the wainscot on the west side of the chamber above the three empty slots, possibly intended to hold beams for lowering blocking stones into place. The top of the wainscot on the east side of the antechamber is flat, five cubits above the floor of the chamber.
The horizontal passage system that leads to the king's chamber begins at what is known as the great step, just north of the southern wall of the grand gallery. The edge of this step is at the north-south midline of the pyramid. Petrie carefully measured the length of each of the flooring blocks from the great step to the king's chamber. The lengths are generally in whole numbers of digits and all of the numbers in the diagram below are in digits unless otherwise specified.
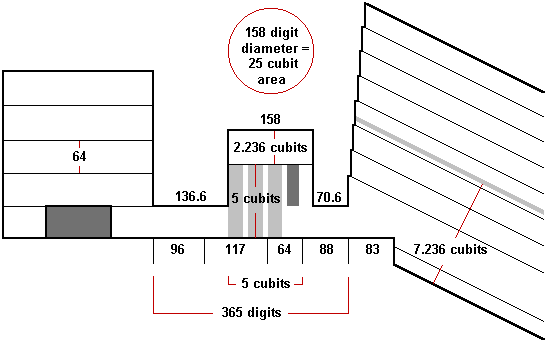
The distance from the edge of the great step at the midline of the pyramid to the northern wall of the king's chamber is 448 digits or 16 cubits. According to Petrie, the distance from the beginning of the antechamber passage at the south wall of the gallery to the end of the king's chamber passage at the north wall of the king's chamber is 269.1 inches. This converts to 365.2 digits, a precise expression of the number of days in a year.
Petrie gives the height of the antechamber as 149.3 inches (7.236 cubits). The height of the east wainscot is five cubits and the height of the upper portion of the chamber is 2.236 cubits. The height of the king's chamber is equal to five times 2.236 while the height of the antechamber is equal to five plus 2.236. The 158 digit length of the antechamber divided by 2.236 gives the 70.6 digit length of the antechamber passage. The 7.236 cubit height of the antechamber is the same as the transverse height of the gallery up to the point of the groove in the third overlap. The upper width of the antechamber is 22 palms or 3.14 cubits. The width of the gallery at the height of the third overlap is also 22 palms. The limestone floor block that goes from the beginning of the antechamber passage into the antechamber is also 22 palms, or 88 digits, or 3.14 cubits long. The first granite flooring block in the antechamber is 64 digits, or 16 palms long. This is the same length as the height of the courses in the king's chamber and the same length as the transverse height of the descending and ascending passages, and since the width of the floor of the antechamber is 2 cubits, the surface perimeter of this block is the same as the perimeters of the descending and ascending passages. The second granite flooring block is 117 digits, or 4.18 cubits long. This is 1/100th of the ridge length of 418 cubits from the corner of the pyramid at ground level to the apex of the pyramid. 4.18 also closely approximates 4/3π. The granite portion of the floor of the antechamber is five cubits long, so the five by five square represented by the portion of the east wainscot above the granite portion of the floor has the same 25 cubit area as a circle with a diameter equal to the 158 digit length of the antechamber.
1. WMF Petrie, The Pyramids and Temples of Gizeh, (1883).
2. Rudolph Gantenbrink, http://www.cheops.org, (1999).
3. John Legon, 'The Air-Shafts in the Great Pyramid', Discussions in Egyptology 27 (1993), 35-44;'Air-Shaft Alignments in the Great Pyramid', DE 28 (1994), 29-34, also reproduced on his website. Legon proposed that the upper northern shaft and the lower northern shaft as extended would merge at the height of the apex of the Great Pyramid, 198 cubits across from the point where the upper northern shaft exits the pyramid. Legon also assigned simple fractional slopes to the angles of the shafts in the Great Pyramid, and his slopes for the upper shafts are the same as those used here. Legon also concluded that the lower shafts were intended to have the same angle. However, Legon assigned a slope of 14/17 to the lower shafts. This translates to an angle of 39° 28' which is closer to Gantenbrink's findings for the lower southern shaft than the slope of 9/11 that is proposed here (equal to an angle of 39° 17'). The point where the lower northern shaft begins it's ascent inside the pyramid is 44 cubits above ground level and 8.7 cubits north of the centerline of the pyramid. From this point to the point where the shaft merges with the upper northern shaft is 288.3 cubits across and 236 cubits up. This corresponds with the slope of 9/11 proposed here. None of the other symmetries of the lower shafts shown here are present given Legon's proposed slope of 14/17. Additionally, Lee McGiffen pointed out that the ratio of 9/11 is also expressed by the exit points of the upper shafts, 126 cubits below the apex and 154 cubits above ground level (126/154 = 9/11). Finally, the 9/11 slope is also seen in the siteplan, in the diagonal that defines the area of the three major pyramids at Giza, from the NE corner of the first pyramid to the SW corner of the third pyramid.
4. Robin Cook, 'The Stellar Geometry of the Great Pyramid'. Discussions in Egyptology. 29. (1994), also reproduced in part on his website. Cook diagrammed the southern shafts merging vertically under the exit point of the upper northern shaft but he subsequently dismissed this finding based on Gantenbrink's report of the angle of the lower southern shaft. Although Gantenbrink has produced the best evidence to date regarding the angle of the lower southern shaft, his finding was based on inconsistent measurements of less than one half of the length of the shaft over portions of the floor that were broken and uneven. Given that his survey findings for both of the lower shafts are in very close proximity to the proposed 9/11 slope, the overall symmetry and consistencey of the plan that results from the application of this slope shows that it was the intended specification for the lower shafts.
5. www.aiwaz.net, Great Pyramid dimensions
6. Rick Howard, The e proportion
7. Paul Calter